Adding Calculus to the Scene
Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 20, 2025
![]()
Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 20, 2025
![]()
Right after the NO TRIGONOMETRIC PROOF paragraphs (please see this page), Loomis made another bold move by claiming that [calculus] furnishes no new proof as shown below. This is certainly not true. For example, Paul Maiorano's Proof using analytic geometry does prove the Pythagorean Identity, even though the proof can be considered as a variation of the classical proofs based on similar triangles. On the other hand, calculus is a very different story, because the introduction of limits, differentiation and integration changed the game significantly.

|
The following diagram illustrates the relationship among calculus, analytic geometry and the classical Euclidean geometry. It is not entirely accurate, but it is good enough for our purpose. The classical Euclidean geometry is extended by adding coordinates to analytic/coordinate geometry. The added coordinates allow us to do many things that are difficult or even impossible to do. The concepts of homogeneous coordinates, imaginary numbers, circular points, isotropic lines, line coordinates, trilinear coordinates, etc. are good examples. By adding the concept of limits, calculus extends the analytic geometry and, as a result, we have more tools to use such as differentiation, integration, L'Hôpital's Rule, power series, Eucler's formula, ordinary differential equations, etc.
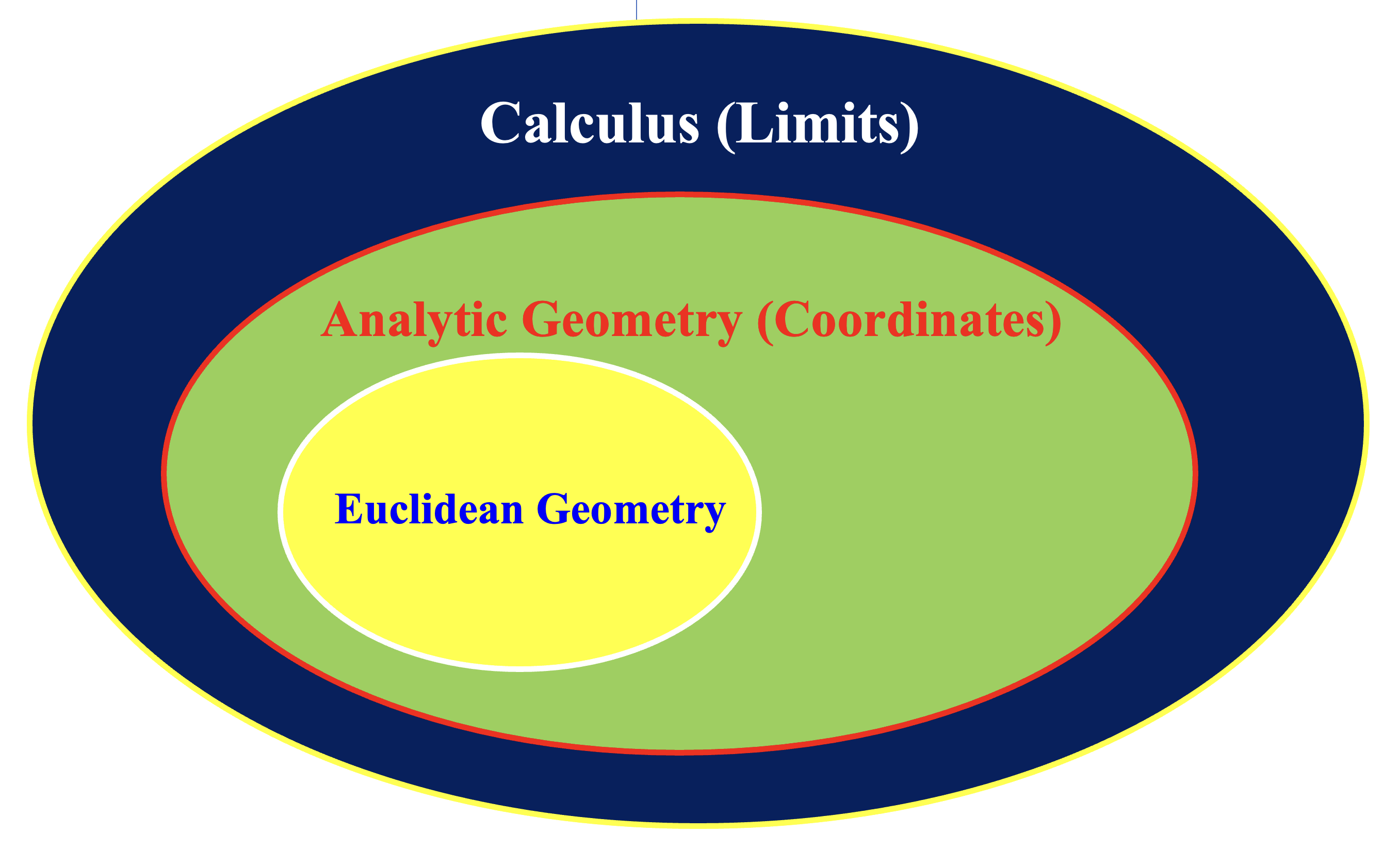
|
The key question is: Are these new tools independent of the Pythagorean Theorem and the Pythagorean Identiy? From the development of calculus, we know that the theory of differentiation and integration are independent of the Pythagorean Theorem and the Pythagorean Identiy. So do the development of power series, Euler's formula, L'Hôpital's Rule, etc. What we need to do is mainly proving the computation of the derivatives of the sine and cosine functions are independent of the Pythagorean Theorem and the Pythagorean Identiy.
Hence, the remaining work is proving that differentiation, integration, etc. with respect to the sine and consines functions are independent of the Pythagorean Theorem and the Pythagorean Identity. This is the main goal of the next few pages.
Go back to Home Page.