A Few Useful Results

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 25, 2025

Before we proceed to present you proofs using caluclus, we need a few more useful results that will be used to prove the Pythagorean Identity using calculus.

Proof of \( x > \sin(x) \)

We first prove an important property \( x > \sin(x) \) to be used in computing the derivatives of the sine and cosine functions without using the Pythagorean Theorem and the Pythagorean Identity.

Let \( O \) be the center of a unit circle and \( \overrightarrow{OC} \) be the x-axis where \( C \) is on the circle (diagram below). Let \( A \) be a point on the circle with \( \angle AOC = x \). Because we are dealing with the limit of \( x \rightarrow 0 \), we may assume that \( x \) is positive and close to 0. The case of a negative \( x \) can be treated similarly. Let \( B \) be the perpendicular foot from \( A \) to the x-axis. From \( \bigtriangleup AOB \) we have \( \overline{OB}=\cos(x) \) and \( \overline{AB} = \sin(x) \). Then, the arc length \( x \) between \( A \) and \( C \) is larger than \( \overline{AC} \), which is the hypotenuse of the right triangle \( \bigtriangleup ABC \) and is larger than the other sides. Therefore, we have \( x > \overline{AC} > \overline{AB} = \sin(x) \).

Proof of \( x > \sin(x) \)

Functions \( \sin(x) \) and \( \cos(x) \) Are Continuous

We shall prove that the function \( \cos(x) \) is continuous. As a result, we have \( \lim_{x\rightarrow 0} \cos(x)=\cos(0)=1 \). The \( \epsilon-\delta \) notation is used. Given any \( \epsilon > 0 \), let \( \delta = \epsilon \). For any \( a \), if \( |x-a| < \delta \), then the following holds: $$ \begin{eqnarray*} |\cos(x)-\cos(a)| &=& \left| -2\sin\left(\frac{x+a}{2}\right)\sin\left(\frac{x-a}{2}\right)\right| \\ &\leq& 2\cdot 1 \left| \sin\left( \frac{x-a}{2} \right) \right| \\ &<& 2\left| \frac{x-a}{2} \right| \\ &=& |x-a| < \delta =\epsilon \end{eqnarray*} $$ Therefore, \( \cos(x) \) is continuous at \( a \) and \( \lim_{x\rightarrow 0}\cos(x) = \cos(a) \). Note that the above used a Sum-to-Product identity and \( | \sin(x) | \leq 1 \).

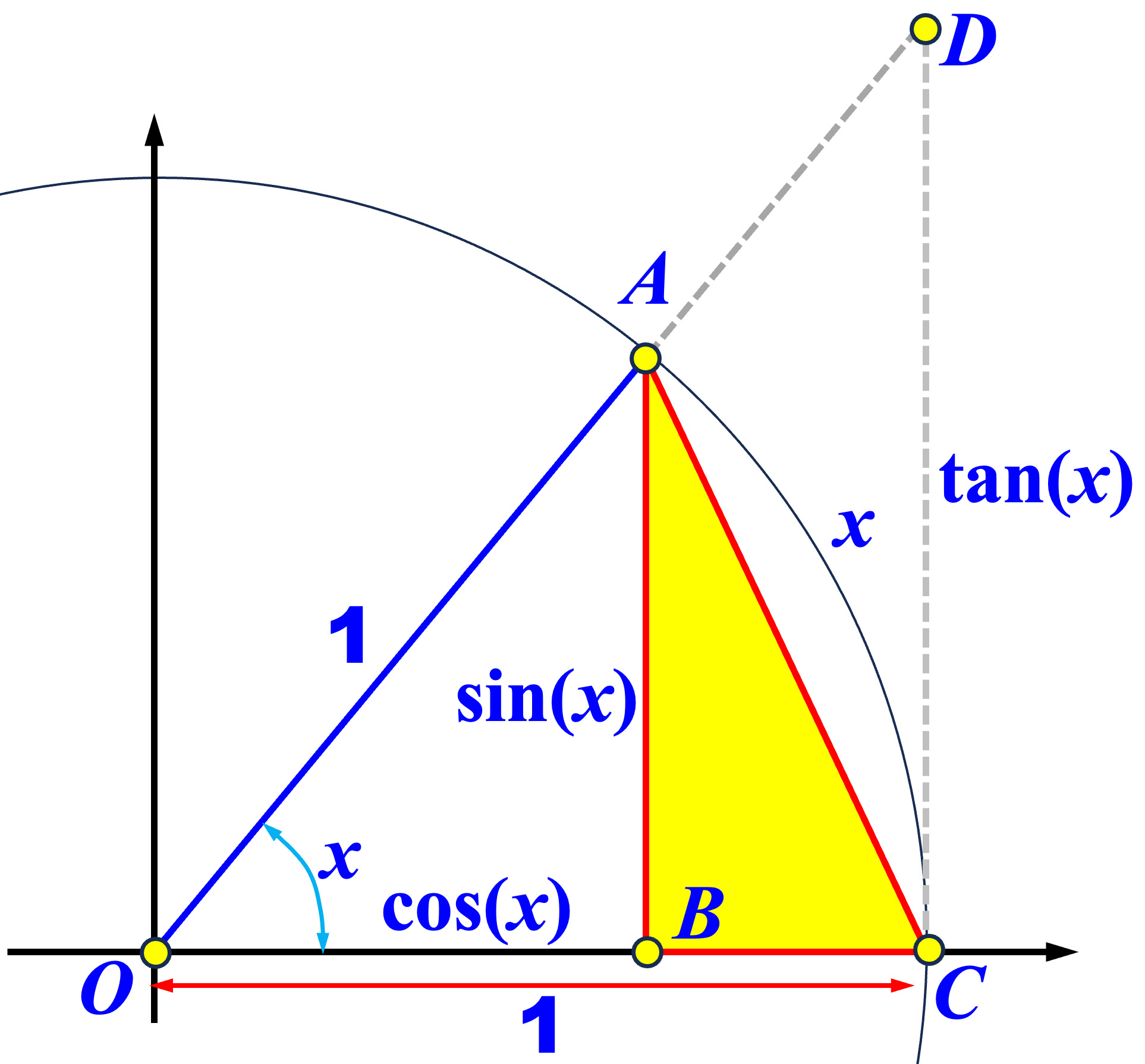
Because \( \sin(x)=\cos\left(\frac{1}{2}\pi - x \right)\), \( \sin(x) \) is also continuous.

Proof of \( \lim_{x\rightarrow 0}\frac{\sin(x)}{x} = 1 \)

Extend \( \overrightarrow{OA} \) so that it meets the line through \( C \) and perpendicular to the x-axis at \( D \). In this way, we have \( \tan(x) = \overline{CD} \) and the area of \( \bigtriangleup ODC \) is \( \frac{1}{2}\tan(x) \). The area of \( \bigtriangleup AOB \) is \( \frac{1}{2}\sin(x)\cos(x) \). The area of the wegde bounded by the arc \( x \) and \( O \) is \( \pi\left( \frac{x}{2\pi} \right) = \frac{1}{2}x \). It is obvious that the area of \( \bigtriangleup DOC \) is larger than the area of the slice of the circle bounded by \( x \), which in turn is larger than the area of \( \bigtriangleup AOB \). As a result, the following holds: \[ \frac{1}{2}\tan(x) = \frac{1}{2}\cdot\frac{\sin(x)}{\cos(x)} > \frac{1}{2}x > \frac{1}{2}\sin(x)\cos(x) \] Simplifying and rearranging gives \[ \cos(x) < \frac{\sin(x)}{x} < \frac{1}{\cos(x)} \] Because \( \cos(x) \) is continuous, we have \( \lim_{x\rightarrow 0} \cos(0) = 1 \) and hence \( \lim_{x\rightarrow 0} \frac{\sin(x)}{x} = 1 \).

Proof of \( \lim_{x\rightarrow 0}\frac{1-\cos(x)}{x} = 0 \)

Then, we shall prove \( \lim_{x\rightarrow 0}\frac{1-\cos(x)}{x} = 0 \). The following diagram was used in the discussion of Luzia's 2015 proof. We proved the following on that page: $$ \begin{eqnarray*} \overline{BC} &=& 1-\cos(x) \\ \overline{AC} &=& 2\sin\left(\frac{x}{2}\right) \\ \varphi &=& 90^{\circ}-\frac{x}{2} \\ \cos(\varphi) &=& \sin\left( \frac{x}{2} \right) \end{eqnarray*} $$ From right triangle \( \bigtriangleup ABC \) we also have \[ \overline{BC} = \overline{AC}\cdot\cos(\varphi) = \left( 2\sin\left(\frac{x}{2} \right) \right) \cdot \sin\left( \frac{x}{2} \right) = 2\sin^2\left( \frac{x}{2} \right) \] Therefore, the following holds: \[ 1-\cos(x) = \overline{BC} = 2\sin^2\left( \frac{x}{2} \right) \] In this way, we have $$ \begin{eqnarray*} \lim_{x\rightarrow 0}\frac{1-\cos(x)}{x} &=& \lim_{x\rightarrow 0} \frac{2\sin^2\left(\frac{x}{2}\right)}{x} = \lim_{x\rightarrow 0} \frac{\sin^2\left(\frac{x}{2}\right)}{\frac{x}{2}} = \lim_{x\rightarrow 0} \left[ \frac{\sin\left(\frac{x}{2}\right)}{\frac{x}{2}} \cdot\sin\left(\frac{x}{2}\right) \right] \\ &=& \lim_{x\rightarrow 0} \left[ \frac{\sin\left(\frac{x}{2}\right)}{\frac{x}{2}} \right] \cdot\lim_{x\rightarrow 0} \sin\left(\frac{x}{2}\right) = 1\cdot 0 = 0 \end{eqnarray*} $$

Proof of \( \lim_{x\rightarrow 0}\frac{|\ln(\cos(x))|}{x} = 0 \)

This proof is a little more complex and uses the property of the \( \ln() \) function being concave for all \( x > 0 \).

Recall the weighted AM-GM (arithmetic mean - geometric mean) inequality. Given non-negative \( x \) and \( y \) and a non-negative weight \( 0 \leq \lambda \leq 1 \), the weighted AM-GM inequality means \( \lambda x + (1-\lambda) y \geq x^{\lambda} \cdot y^{1-\lambda} \). For the \( \ln() \) function we have $$ \begin{eqnarray*} \ln( \lambda x + (1-\lambda) y ) &\geq& \ln\left( x^{\lambda} \cdot y^{1-\lambda} \right) \\ &=& \ln\left(x^{\lambda}\right) + \ln\left(y^{1-\lambda} \right) \\ &=& \lambda\ln(x) + (1-\lambda)\ln(y) \end{eqnarray*} $$ This means the natural logarithm function \( \ln() \) is a concave function.

Now, consider the unit circle with center \( O \) at the coordinate origin. The curve of \( \ln() \) passes through the point \( C = (1,0) \) (diagram below). Note that the slope of the tangent of \( \ln() \) at \( C \) is 1 and passes through the south pole \( S = (0,-1) \) of the unit circle. Because the curve of \( \ln() \) is concave, it is below the line \( \overleftrightarrow{CS} \). Furthermore, the curve of \( \ln() \) enters the unit circle from \( C \) and exits the unit circle at a point \( W \). Let the line through \( W \) and perpendicular to \( \overleftrightarrow{OC} \) meet \( \overleftrightarrow{OC} \), \( \overleftrightarrow{SC} \) and the unit circle (again) at \( U \), \( V \) and \( T \), respectively. Consequently, the curve of \( \ln() \) lies completely inside the triangle \( \bigtriangleup CVW \).

Let \( \varphi = \angle TOU \). Let \( A \) be a point on the unit circle. If \( \theta = \angle AOC > \varphi \), the line through \( A \) and perpendicular to \( \overleftrightarrow{OC} \) does not interset the curve of \( \ln() \) in \( \bigtriangleup CVW \). Hence, we are safe to assume that \( \theta \leq \varphi \). Let the line through \( A \) and perpendicular to \( \overleftrightarrow{OC} \) meeting \( \overleftrightarrow{OC} \), \( \overleftrightarrow{SC} \), the curve of \( \ln() \), \( \overleftrightarrow{WC} \) and the unit circle (again) at \( B \), \( D \), \( E \), \( F \) and \( G \). In this way, we have the following: $$ \begin{eqnarray*} \overline{OB} &=& \cos(\theta) \\ \overline{BC} &=& \overline{BD} = 1-\cos(\theta) \\ \overline{BE} &=& |\ln(\overline{OB})| = |\ln(\cos(\theta))| \end{eqnarray*} $$

The diagram below is a portion of the diagram above. Consider \( \bigtriangleup CVW \). Because \( \bigtriangleup CUW \sim \bigtriangleup CBF \) and \( \bigtriangleup CUV \sim \bigtriangleup CBD \), we have \[ \frac{\overline{UW}}{\overline{UV}} = \frac{\overline{BF}}{\overline{BD}} \] Let \( \rho = \frac{\overline{UW}}{\overline{UV}} \). Note that \( \rho > 1\) is a constant because \( \varphi \) is a constant. Therefore, we have \( \overline{BF} = \rho\cdot\overline{BD} \) and \( \overline{BF} \geq \overline{BE} \geq \overline{BD} \). The following holds: \[ \overline{BF} = \rho\cdot\overline{BD} \geq \overline{BE} \geq \overline{BD} \] Because \( \overline{BD} = 1-\cos(\theta) \), the above becomes \[ \rho(1-\cos(\theta)) \geq | \ln(\cos(\theta) |\geq 1-\cos(\theta) \] Dividing the above by \( \theta \) yeilds \[ \rho\frac{1-\cos(\theta)}{\theta} \geq \frac{| \ln(\cos(\theta) |}{\theta} \geq \frac{1-\cos(\theta)}{\theta} \] Because \( \lim_{x\rightarrow 0}\frac{1-\cos(\theta)}{\theta} = 0 \), we have \[ \lim_{x\rightarrow 0}\frac{|\ln(\cos(\theta))|}{\theta} = 0 \]

In fact, the absolute value in the above result does not matter because the limit is 0.

Go back to Home Page.