Coordinate Axes Rotation

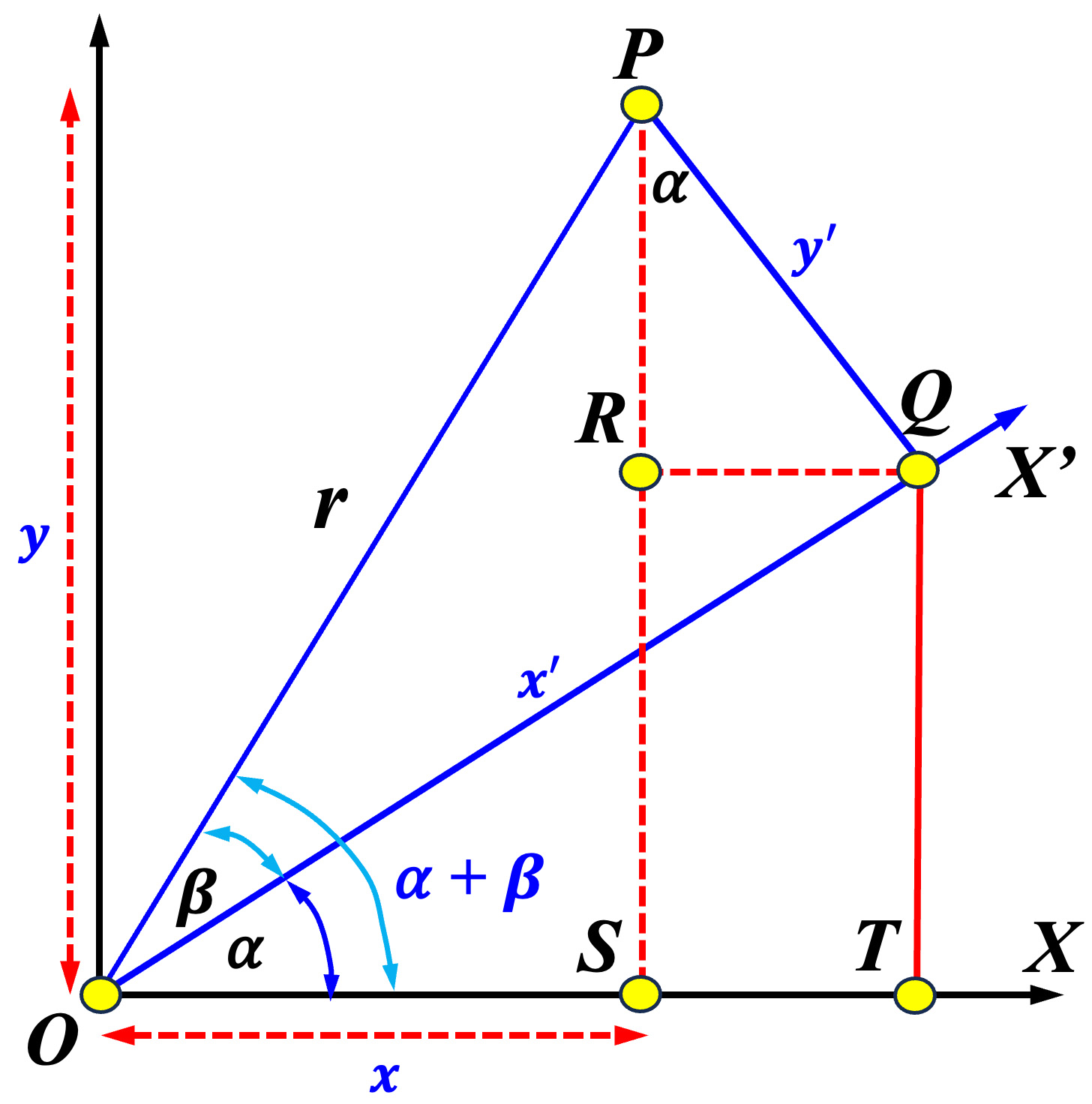
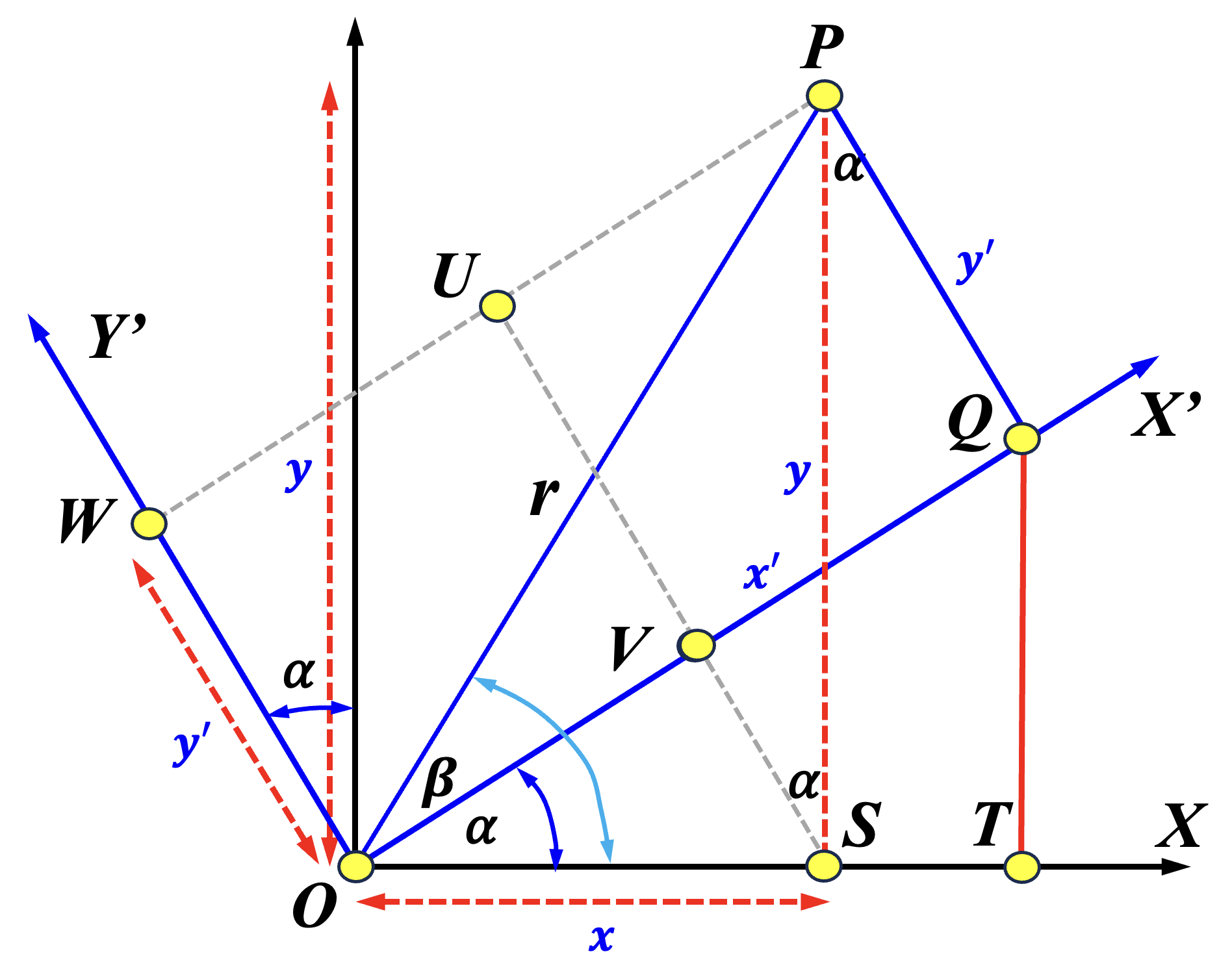
The angle sum identities are used to derive the coordinate axes rotation from the X'Y' system to the XY system as follows: $$ \begin{eqnarray*} x^{\prime} &=& r\cos(\beta) = r\cos((\alpha+\beta)-\alpha)=[r\cos(\alpha+\beta)]\cos(\alpha) + [r\sin(\alpha+\beta)]\sin(\alpha) \\ &=& x\cos(\alpha)+ y\sin(\alpha) \\ y^{\prime} &=& r\sin(\beta)= r\sin((\alpha+\beta)-\alpha)=[r\sin(\alpha+\beta)]\cos(\alpha) - [r\cos(\alpha+\beta)]\sin(\alpha) \\ &=& x\cos(\alpha)- y\sin(\alpha) \end{eqnarray*} $$ Now, if we use \( u = \alpha + \beta \), \( v = \alpha \), we have \( x^{\prime} = r\cos(u-v) \), \( y^{\prime} = r\sin(u-v) \), \( x = \cos(u) \) and \( y = r\sin(v) \). Plugging these into the above coordinate axes rotation equations, we have the angle difference identities.

Therefore, the angle sum and angle differences identities are closely related to the coordinate axes rotation formulation. The proofs of these relations DO NOT need the Pythagorean Theorem. Consequently, Zimba's proof discussed on the angle difference and angle sum identities page is not new and has been a typical topic in a coordinate/analytic geometry textbook.

There is a commonly seen proof of the relations from \( (x,y) \) to \( (x^{\prime},y^{\prime}) \). For example, A. Robson's An Introduction to Analytical Geometry, Volume 1, pp. 37--38, includes such a proof. Please refer to the right diagram above. It is essentially the same as the left one with the Y'-axis shown. Let the pendicular foot from \( P \) to the Y'-axis be \( W \), let the perpendicular foot from \( S \) to \( \overleftrightarrow{PW} \) be \( U \) and let \( \overleftrightarrow{PW} \) meet the X'-axis at \( V \). Now we have the following: $$ \begin{eqnarray*} x^{\prime} &=& \overline{OQ}=\overline{OV}+\overline{VQ}=\overline{OV}+\overline{UP} = x\cos(\alpha)+y\sin(\alpha) \\ y^{\prime} &=& \overline{PQ}=\overline{OW}=\overline{UV}=\overline{US}-\overline{VS} = y\cos(\alpha)-x\sin(\alpha) \end{eqnarray*} $$ Just like what we did above, if we use \( u = \alpha + \beta \), \( v = \alpha \), we have \( x^{\prime} = r\cos(u-v) \), \( y^{\prime} = r\sin(u-v) \), \( x = \cos(u) \) and \( y = r\sin(v) \).

Most coordinate/analytic geometry book only discussed the transformation from \( (x,y) \) to \( (x^{\prime},y^{\prime}) \) and did not work the transformation from \( (x^{\prime},y^{\prime}) \) to \( (x,y) \). Usually, the authors either skipped this topic or simply stated like ``by the same reason or the same techniques.'' Some textbook treated this as computing the inverse of the transformation \( (x,y) \) to \( (x^{\prime},y^{\prime}) \); however, in doing so the Pythagorean Identity is used.

I found an even earlier analytic geometry textbook by Osmar Fort, Lehrbuch der Analytischen Geometrie. My copy is the third edition published in 1872. The Preface of the second edition shows the year of 1863. Therefore, the first edition should be even earlier. This book uses the oblique coordinate system, which means that the angle between the x-axis and the y-axis does not have to be \( 90^{\circ} \). The following diagrams show page 22 and page 23, on which the coordinate transformation from \( (x,y) \) to \( (x^{\prime},y^{\prime}) \) is discussed.

Let us take how the transformation is calculated. The given coordinate system is XY, which is to be transformed to the new coordinate system X'Y' system. Let \( P \) is a point with coordinates \( (x,y) \) and \( (x^{\prime},y^{\prime}) \) in the XY and X'Y' systems, respectively. Let \( \overleftrightarrow{PR} \) be a line parallel to the Y'-axis, where \( R \) is a point on the X'-axis. Let \( S \) be the perpendicular foot from \( R \) to the X-axis, let \( T \) be the perpendicular foot from \( P \) to the X-axis, and let \( Q \) be the perpendicular foot from \( R \) to \( \overleftrightarrow{PT} \). Let the angle between the X-axis and the X'-axis be \( \alpha \) and let the angle between the X-axis and the Y'-axis be \( \beta \). Then, \( \angle PRQ = \beta \). In this way, we have \( x = \overline{OT} \), \( y = \overline{PT} \), \( x^{\prime} = \overline{OR} \) and \( y^{\prime} = \overline{PR} \).

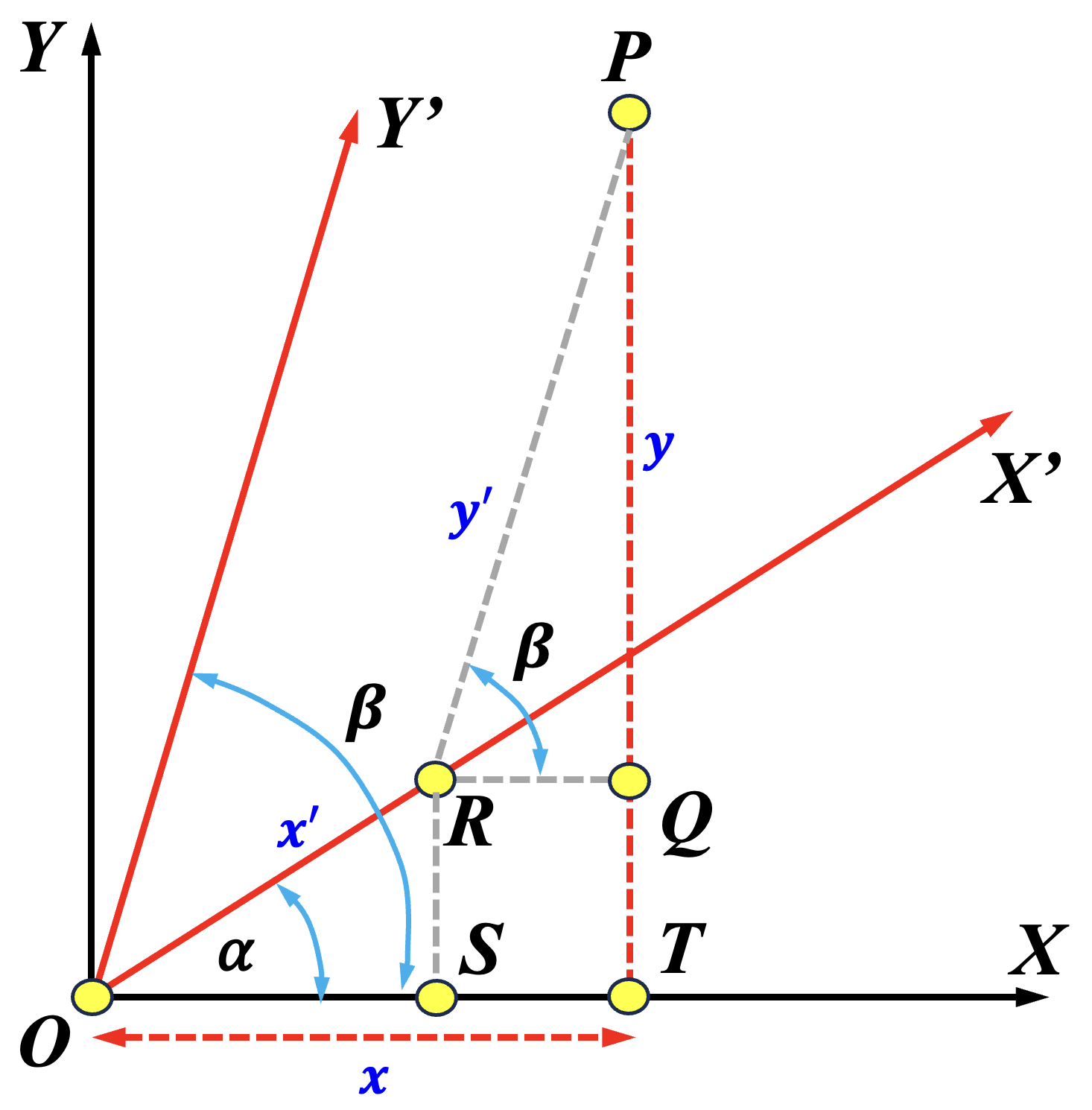
Given these values, we have $$ \begin{eqnarray*} x &=& \overline{OS}+\overline{ST} = x^{\prime}\cos(\alpha)+\overline{RQ} =x^{\prime}\cos(\alpha) + y^{\prime}\cos(\beta) \\ y &=& \overline{PQ}+\overline{QT} = x^{\prime}\sin(\alpha)+ y^{\prime}\sin(\beta) \end{eqnarray*} $$ If the X'Y' system is also rectangular, we have \( \beta = \alpha + 90^{\circ} \). Thus, \( \cos(\beta) = -\sin(\alpha) \) and \( \sin(\beta)=\cos(\alpha) \). Plugging these into the above results, we have the coordinate axes rotaton equations, and hence, the angle difference identities are obtained. Note that this is stated on page 23 of Fort's 1872 book. Also note that this proof is not very different from the one shown at the beginning of this page.

What did we learn here?
We showed that the angle difference and angle sum identities for sine and cosine can be proved without using the Pythagorean Theorem or Pythagorean Identity, and, as a result, the Pythagorean Identity can be proved from either one without circular reasoning. Then, we showed that in a 1899 book of analytic geometry by Friedrich Schur not only the Pythagorean Identity can be proved without using the Pythagorean Theorem, but also the angle difference and angle sum identities can be linked to coordinate axes rotation as shown on this page. This clearly shows that the proofs of the Pythagorean Theorem, and hence the Pythagorean Identity, was proved long before Zimba and Jackson-Johnson did in 2009 and 2023, respectively.

Loomis indicated that the proof of the Pythagorean Theorem in Versluys's 1914 book IS NOT a proof because Versluys used the Pythagorean Idcentity to prove the Pythagorean Theorem. However, Loomis missed the first sentence in Versluys' proof, which indicated that In trigonometry, it is usually shown without the aid of the Pythagorean Theorem that \( \sin(B+C)=\sin(B)\cos(C)+\cos(B)\sin(C) \). Now we know that Loomis was all wrong about the relationships between the fundamental formulae in trigonometry and the Pythagorean Theorem. Additionally, proving the angle difference and angle sum identities without using the Pythagorean Theorem and the Pythagorean Identities was done long before Loomis made his claim, even in the first edition published in 1928. The math community failed to point out that people in the 19th century had already done the same and the materials actually were typical topics in coordnate/analytic geometry.

Finally, we provide links between the angle difference and angle sum identities and coordinate axes rotation here on this page.

I hope these discussions can provide you with a clear picture in the quest for finding proofs of the Pythagorean Theorem using trigonometry. They are already in classical textbooks long before Zimba published his paper in 2029 and Jackson and Johnson presented their "impossible" proof in 2023. You will find more proofs here in the future. Now, let me close this Classical Work chapter and move on to other topics.

Go back to Home Page.