The Angle Difference and Angle Sum Identities for Sine and Cosine

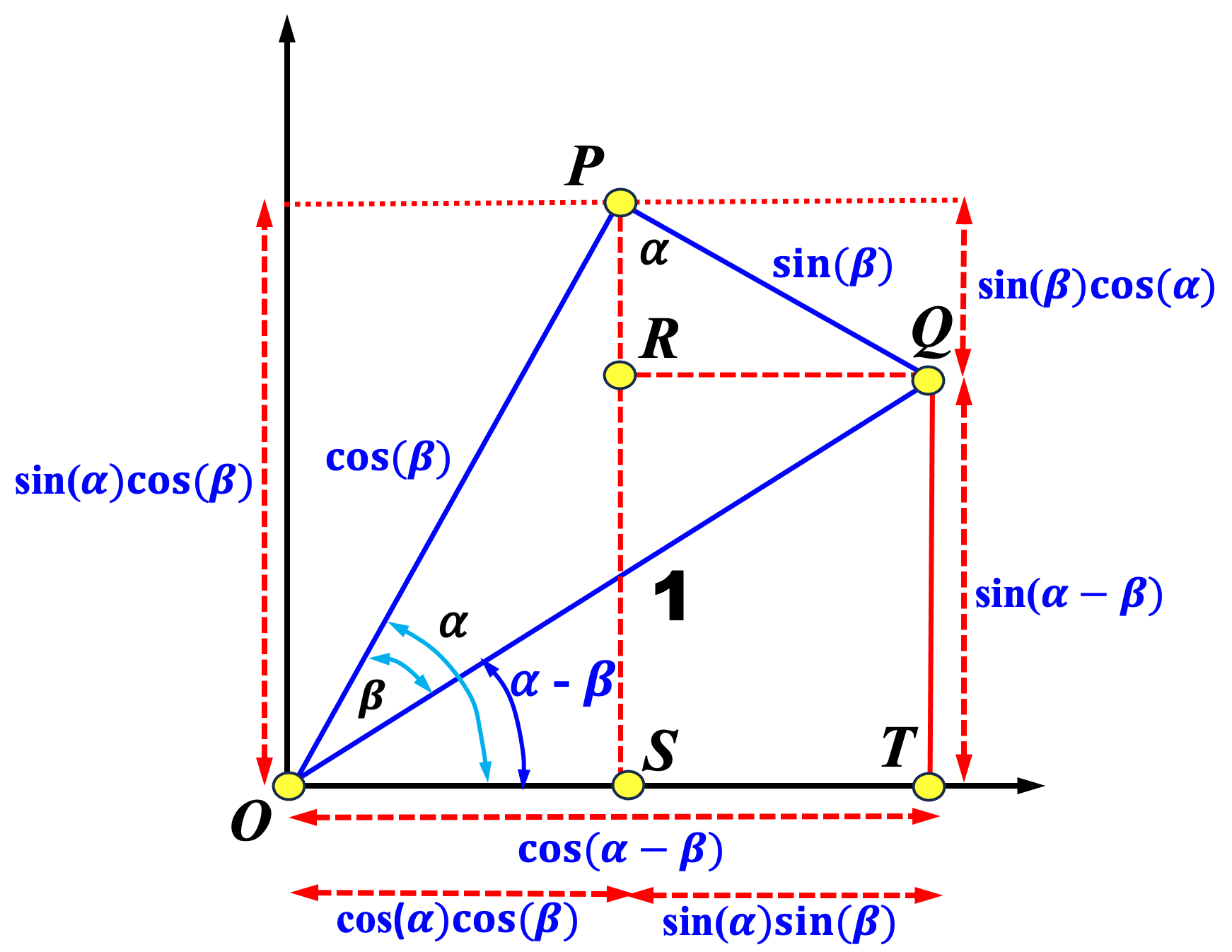
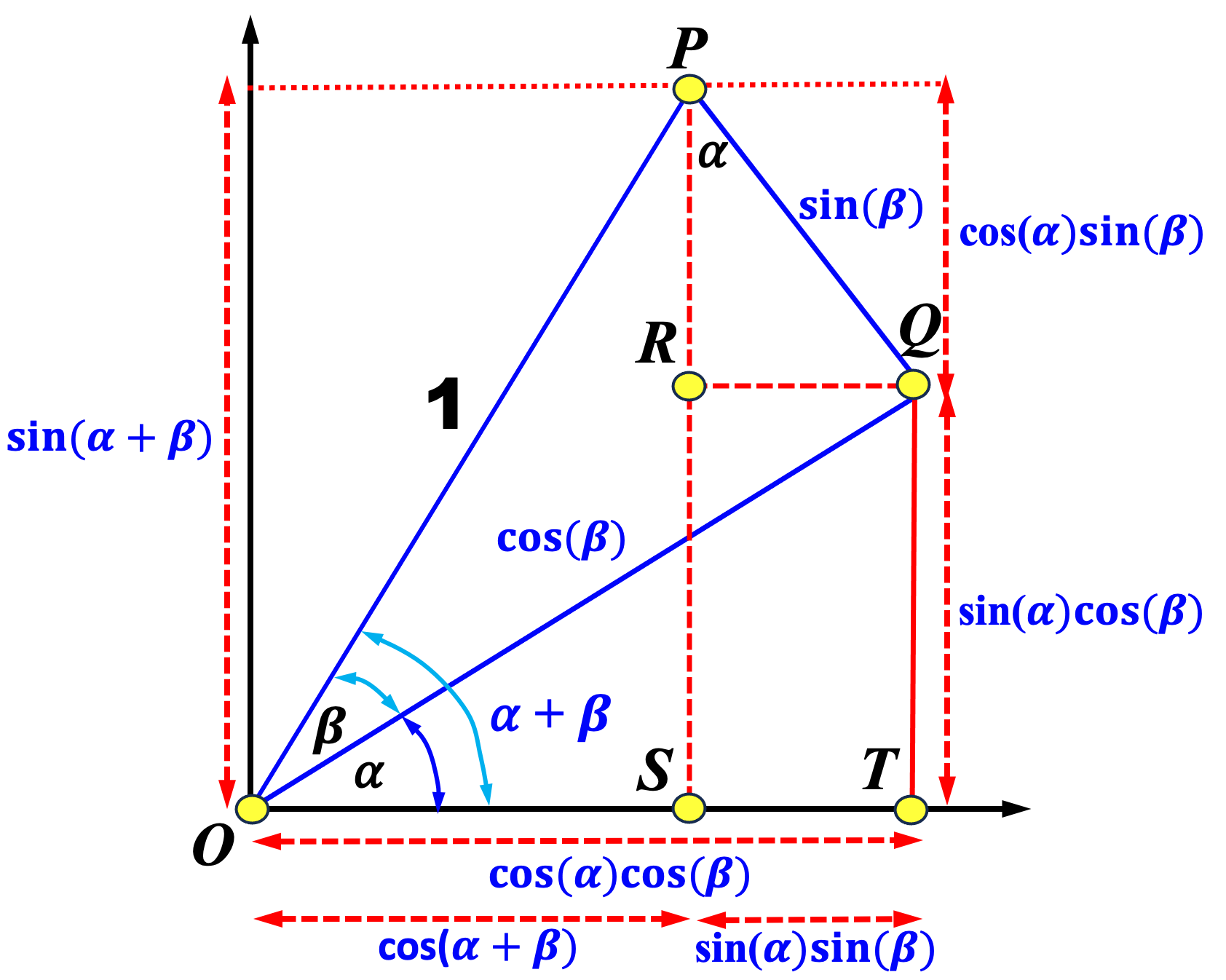
The left diagram above is for the angle difference identities. Let \( \overleftrightarrow{OT} \) be the x-axis, let \( \overleftrightarrow{OP} \) make an angle of \( \alpha \) with \( \overleftrightarrow{OT} \), let \( \overleftrightarrow{OQ} \) make an angle of \( \beta \) with \( \overleftrightarrow{OP} \) and let \( \overline{OQ} = 1 \). Furthermore, let \( P \) be the pendicular foot from \( Q \) to \( \overleftrightarrow{OP} \). In this way, \( \angle QOT = \alpha - \beta \). From the right triangle \( \bigtriangleup OQT \) we have \( \overline{QT}=\sin(\alpha-\beta) \) and \( \overline{OT}=\cos(\alpha-\beta) \). From the right triangle \( \bigtriangleup OQP \) we have \( \overline{PQ}=\sin(\beta) \) and \( \overline{OP}=\cos(\beta) \). Let the perpendicular foot from \( P \) to \( \overleftrightarrow{OT} \) be \( S \) and let the perpendicular foot from \( Q \) to \( \overleftrightarrow{PS} \) be \( R \). From the right triangle \( \bigtriangleup OPS \) we have \( \overline{OS}=\cos(\alpha)\cos(\beta) \) and \( \overline{PS}=\sin(\alpha)\cos(\beta) \). In the right triangle \( \bigtriangleup PQR \) we have \( \angle QPR = \alpha \) and hence we have \( \overline{QR} = \sin(\alpha)\sin(\beta) \) and \( \overline{PR} = \sin(\beta)\sin(\alpha) \). With these results, the angle difference identities for sine and cosine can easily be obtained.

Angle sum identities can be obtained essentially the same way as shown in the right figure above. In the diagram, \( \angle POT = \alpha + \beta \), \( \angle QOT = \alpha \) and \( \angle POQ = \beta \). Furthermore, this time \( Q \) is the perpendicular foot from \( P \) to \( \overleftrightarrow{OQ} \) and \( \overline{OP} = 1 \). The remaining can be obtained easily.

Do you notice the similarity between the diagrams above and the diagrams used in discussing coordinate axes rotation?

That is correct! These diagrams are frequently used in coordinate/analytic geometry textbooks in the sections or chapter regarding coordinate axes rotation. Please refer to the Coordinate Roration page for more details.

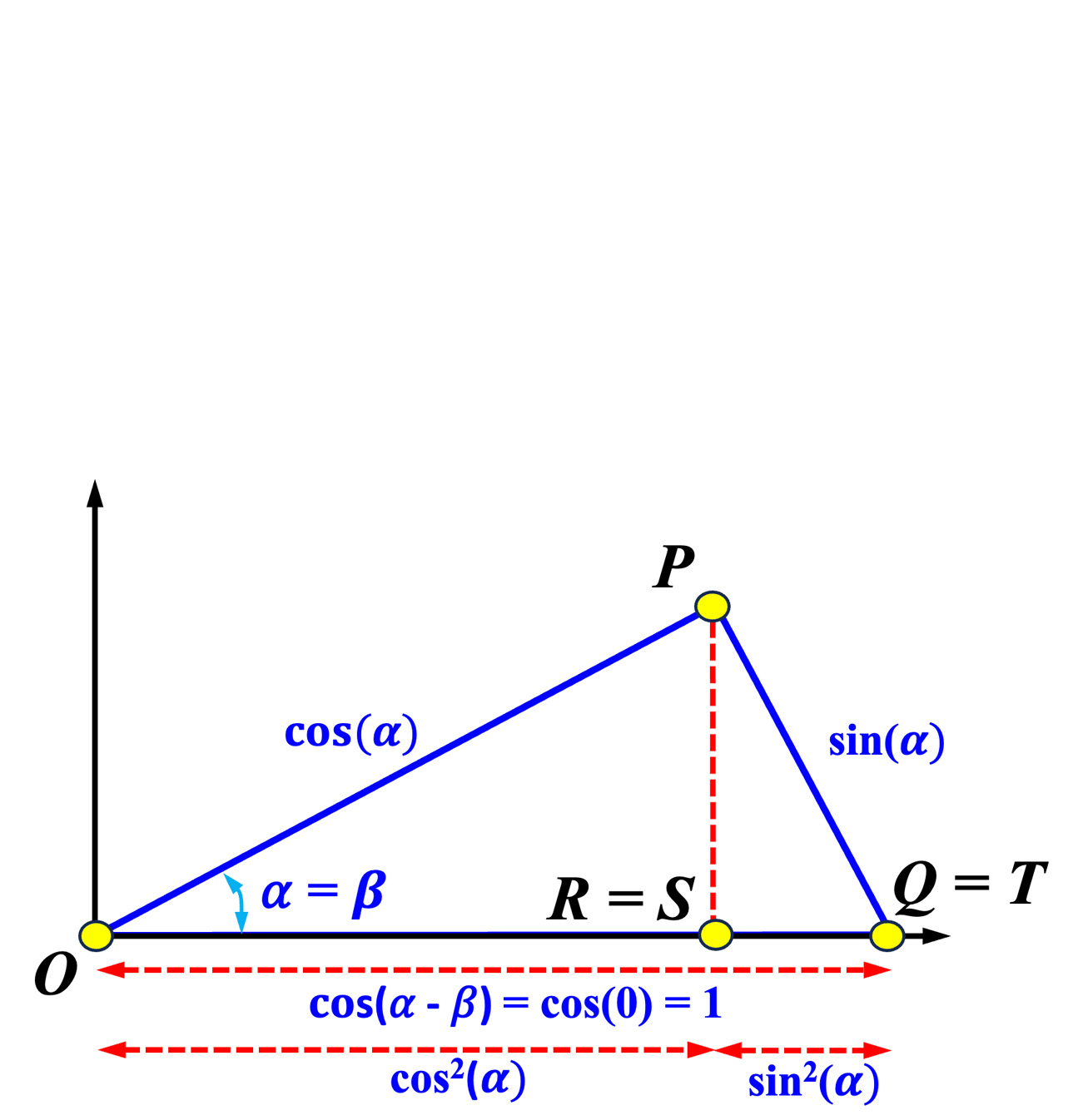
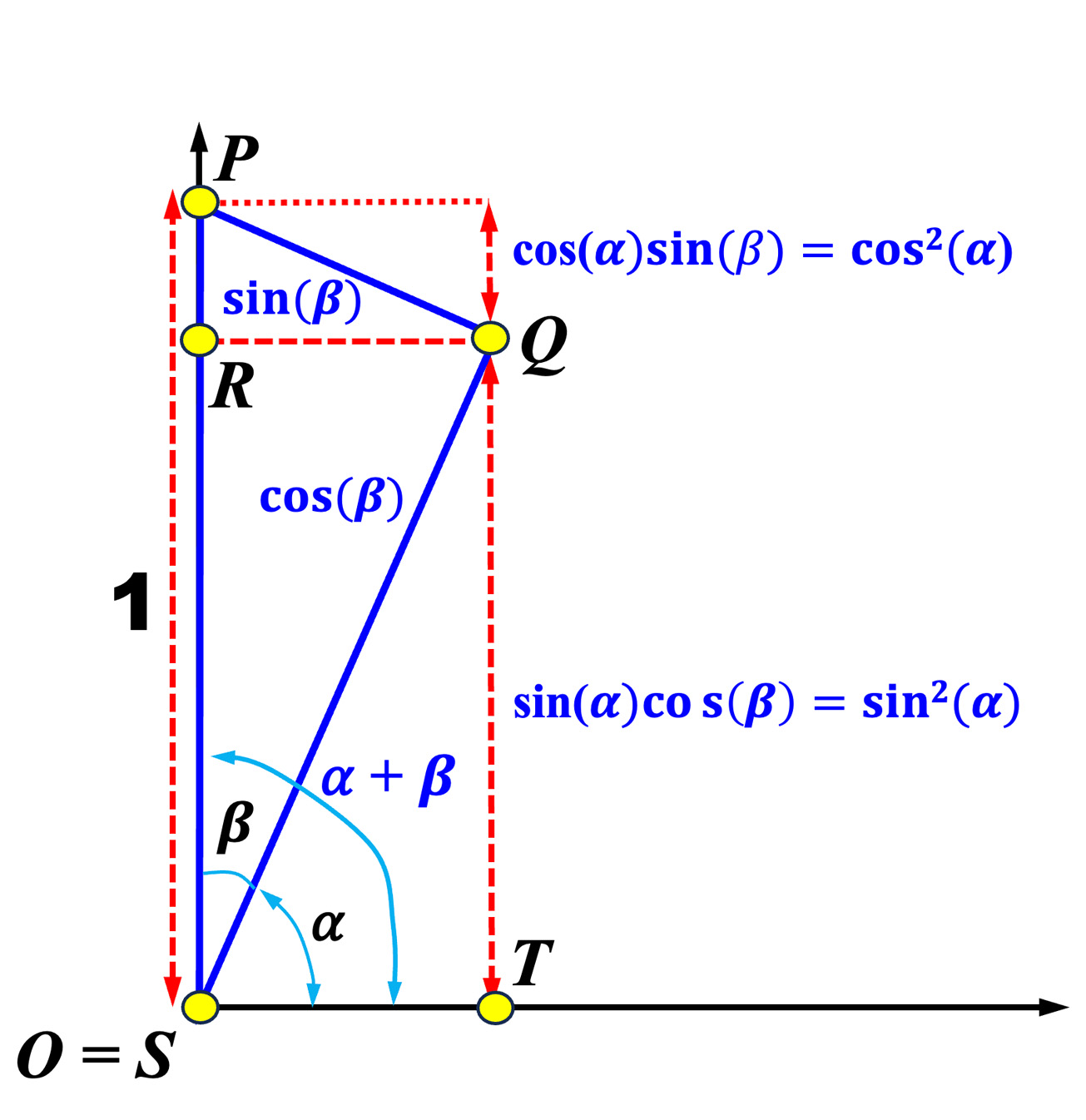
Then, we have to mention two special cases, each of which proves the Pythagorean Identity. For the angle difference identity for cosine (left diagram above), if \( \alpha = \beta \), \( \overleftrightarrow{OQ} \) collapses to \( \overleftrightarrow{OT} \). As a result, we have \( Q=T \), \( R=S \) and \( \overline{OT} = \cos(\alpha - \beta) = \cos(0) = 1 \). In this way, we have the Pythagorean Identity. The right diagram above shows the angle sum case. If \( \alpha+\beta = \frac{1}{2}\pi \), then \( \overleftrightarrow{OP} \) becomes the y-axis. Because \( \overline{OP}=1 \), we have the Pythagorean Identity again. In fact, the diagrams above are the same except for their orientation. In this way, we have two identitical proofs of the Pythagorean Identity.

The above almost trivial proof can easily be proved by Book 6, Proposition 8 in Euclid's The Elements. This type of proofs was popular in elementary geometry textbooks in France in the 19th century, such as Adrien-Marie Legendre's Éléments de Géométrie. However, the real proof in Euclid's The Elements is in Book 6, Proposition 31. In other word, Euclid presented two proofs of the Pythagorean Theorem, one in Book 1, Proposition 47 and the other in Book 6, Proposition 31, the latter being an extension to the Pythagorean Theorem.

Now get back to Zimba's work mentioned earlier. Zimba actually use the same technique to prove the angle difference identities. However, in his theory, the domain and range of the sine and cosine functions are in the open intervals \( \frac{1}{2}\pi \) and \( (0,1) \), respectively. As a result, in his theory by setting \( \alpha = \beta \) or setting \( \alpha + \beta = \frac{1}{2}\pi \) to prove the Pythagorean Identity is problematic as stated in a footnote of his paper:

This footnote mentioned Versluys' work, which will be discussed here. To overcome this domain issue, Zimba used the following to prove the Pythagorean Identity. Given any \( x \in (0,\frac{1}{2}\pi ) \) and any \( y \) with \( 0 < y < x < \frac{1}{2}\pi \), we have \( x, y, x-y \in (0,\frac{1}{2}\pi ) \). Therefore, applying the angle difference identity gives $$ \begin{eqnarray*} \cos(y) &=& \cos(x-(x-y)) = \cos(x)\cos(x-y)+\sin(x)\sin(x-y) \\ &=& \cos(x)[ \cos(x)\cos(y) + \sin(x)\sin(y) ] + \sin(x)[ \sin(x)\cos(y) - \cos(x)\sin(y) ] \\ &=& \left( \cos^2(x) + \sin^2(x) \right) \cos(y) \end{eqnarray*} $$ Because \( \cos(y) \neq 0 \), we have the Pythagorean Identity. Note that the requirement of the involved angles being in \( (0,\frac{1}{2}\pi ) \) is due to Zimba's theory rather than due to the conventional theory of trigonometry. As shown earlier, the angle difference and angle sum identities do not have any requirements on the involved angles.

Go back to Home Page.