Michael Hardy's Proof

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created November 9, 2025

In 1988 Michael Hardy published in The Mathematical Intelligencer a proof based on calculus. Hardy's proof is not completely correct as will be seen later. What Hardy's did was acturally Staring's Proof done in a wrong way. Please also refer to a simplified but more correlated version.

Given a right triangle \( \bigtriangleup ABC \) with \( \angle C = 90^{\circ} \), \( \alpha = \angle BAC \), \( a=\overline{BC} \), \( x=\overline{AB} \) and \( f(x)=y=\overline{AB}\). Extend \( x=\overline{AC}\) to \( \overline{AD} \) so that \( \Delta x = \overline{AD} > 0\). The case of \( \Delta x < 0\) can be handled the same way. Construct a line through \( D \) and parallel to \( \overleftrightarrow{AB} \), and let \( E \) be the intersection point of this line and \( \overleftrightarrow{BC} \).

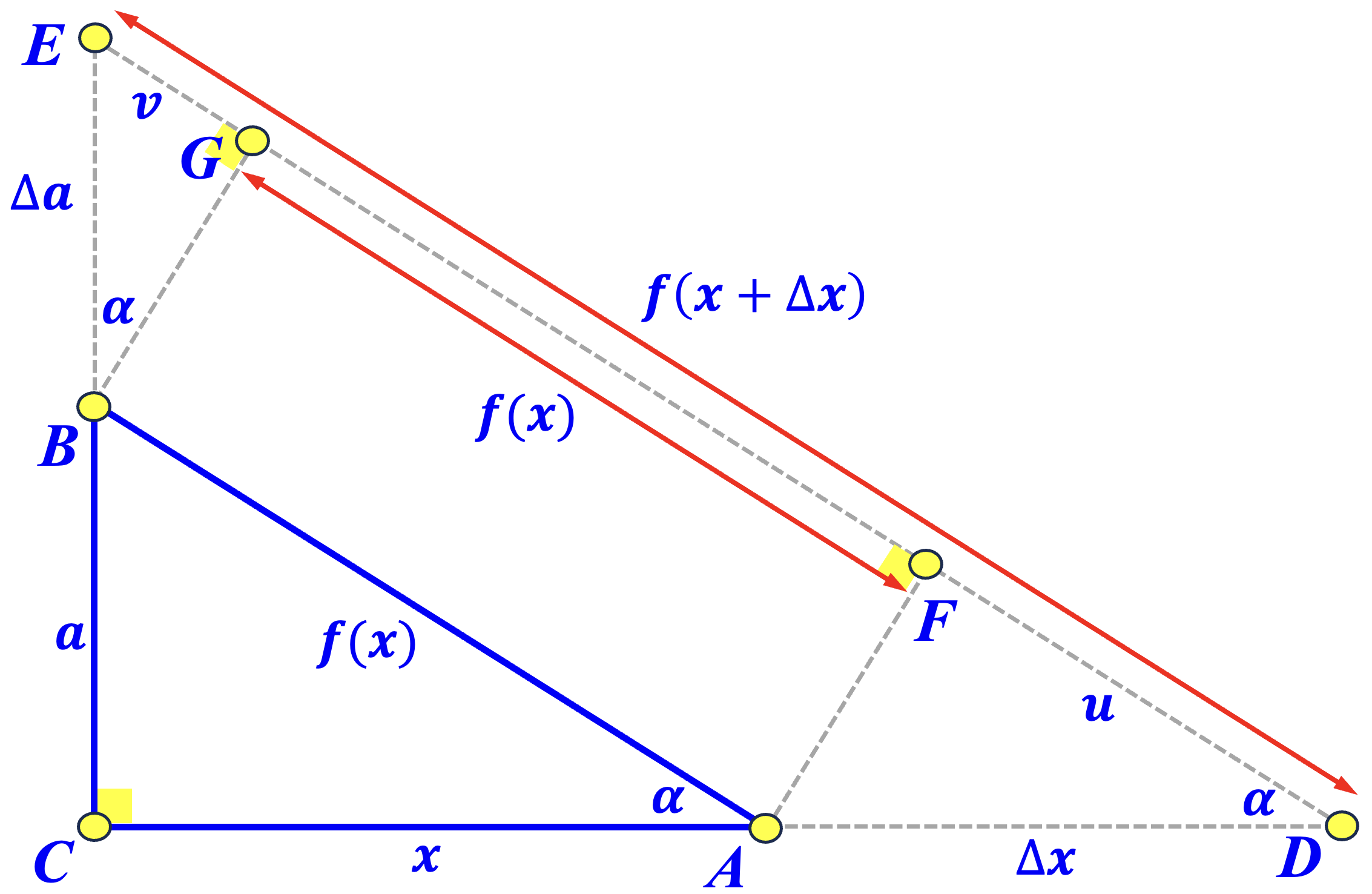
Because \( \bigtriangleup ADF \) is similar to \( \bigtriangleup ABC \), we have \( \frac{u}{\Delta x} = \frac{x}{f(x)} \). Hardy incorrectly claimed that \( u = \overline{FD} \) is \( \Delta y \), the increment/decrement of \( f(x) \) due to \( \Delta x \). As a result, he obtained the following: \[ \frac{dy}{dx} = \frac{\Delta y}{\Delta x} = \frac{u}{\Delta x} = \frac{x}{f(x)} = \frac{x}{y}. \] Solving for \( y \) with initial value \( f(0) = a \), we have \( f^2(x) = y^2 = x^2 + a^2\). This is incorrect because when \( x \) is increased by \( \Delta x \), the increment of \( f(x) \) is not \( u \). In fact, the correct \( f(x) \) increment due to \( \Delta x \) is \( u + v = \overline{FD} + \overline{EG}\).
In the diagram above, if \( x \) is increased by \( \Delta x \), then \( f(x+\Delta x)\) is \( \overline{ED}\). Because going from \( f(x)=\overline{AB} \) to \( f(x+\Delta x) = \overline{DE}\) is linear as \( \Delta x\) increases linearly, it is clear that \( f^{\prime}(x) \) is a constant.
Let us see why. Because \( \bigtriangleup ABC\) is similar to \( \bigtriangleup DEC\), we have the following: \[ \frac{f(x+\Delta x)}{f(x)} = \frac{\overline{DE}}{\overline{AB}} = \frac{\overline{DC}}{\overline{AC}} = \frac{x+\Delta x}{x} = 1+\frac{\Delta x}{x} \] Rearranging and simplifying gives \[ \frac{f(x+\Delta x)-f(x)}{\Delta x} = \frac{f(x)}{x} \] Taking limit gives \[ f^{\prime}(x) = \lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} = \frac{f(x)}{x} = \frac{1}{\cos(\alpha)}=\mbox{costant}. \] Thus, the rate of change is linear, from which the Pythagorean Theorem and the Pythagorean Identity cannot be obtained. This also means that Hardy's proof is incorrect! The main reason as stated earlier is that \( u=\overline{DF}\) is insufficient to cover the change in \( f(x+\Delta x) \) and \( v = \overline{GE} \) must be included. However, once we add \( v = \overline{GE} \), the rate of change becomes linear. Consequently, the simplified version of Staring's proof is not only correct but also more elegant!
Go back to Home Page.