The Angle Sum and Angle Difference Identities for the Tangent Function

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created September 20, 2025

We have shown that the angle sum and angle difference identities are independent of the Pythagorean Theorem and the Pythagorean Identity for the sine and cosine functions. Then, how about the same for the tangent function? Furtunately, they are also independent of the Pythagorean Theorem and the Pythagorean Identity! For example, Suzuki proved the angle difference identity in 1999 and Kung proved the angle sum identity in 2008. Both were published earlier than Zimba's 2009 paper. Nowadays, these proofs are somewhat simplified and frequently found in the form in the diagrams below. The angle difference proof is almost the same (the left diagram below), but the angle sum proof (the right diagram below) is simplified significantly becoming almost trivial. The angle difference proof discussed here is due to Ren in 1999. All of the above mentioned works were published earlier than Zimba's 2009 paper.

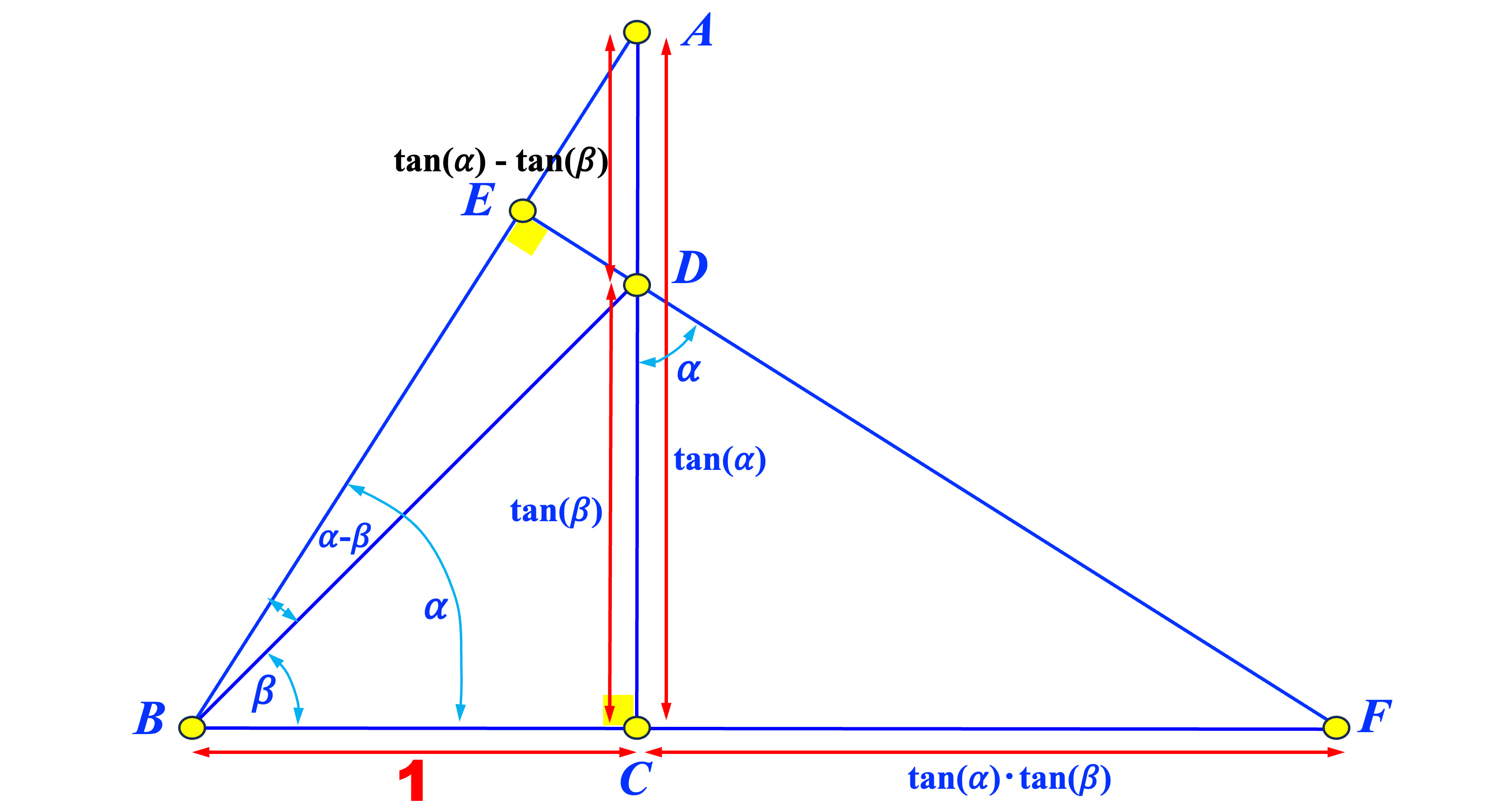
The angle difference identity for the tangent function is proved in the left diagram below. Let \( \bigtriangleup ABC \) be a right trangle with \( \angle C = 90^{\circ} \), \( \angle B = \alpha \) and \( \overline{AB} = 1 \). Pick a point \( D \) on \( \overline{AC} \) so that \( \angle DBC = \beta \) (assuming \( \beta < \alpha \)). In this way, we have \( \angle ABD = \alpha - \beta \). From right triangle \( \bigtriangleup BDC \) we have \( \overline{DC} = \tan(\beta) \). From right triangle \( \bigtriangleup BAC \) we have \( \overline{AC} = \tan(\alpha) \), and hence \( \overline{AD} = \tan(\alpha)-\tan(\beta) \).

Let the line through \( D \) and perpendicular to \( \overleftrightarrow{AB} \) meet \( \overleftrightarrow{AB} \) at \( E \) and \( \overleftrightarrow{BC} \) at \( F \). Note that \( \angle CDF = \angle EDA = \alpha \). From right triangle \( \bigtriangleup CDF \) because \( \frac{\overline{CF}}{\overline{CD}} = \frac{\overline{CF}}{\tan(\alpha)} \) we have \( \overline{CF} = \tan(\alpha)\cdot\tan(\beta) \). Now, we have $$ \begin{eqnarray*} \tan(\alpha-\beta) &=& \frac{\overline{ED}}{\overline{BE}} =\frac{\overline{AD}\cdot\cos(\alpha)}{\overline{BF}\cdot\cos(\alpha)} = \frac{\overline{AD}}{\overline{BF}}\\ &=& \frac{\tan(\alpha)-\tan(\beta)}{1+\tan(\alpha)\cdot\tan(\beta)} \end{eqnarray*} $$ Therefore, the angle difference identity for the tangent function is established. Note that the above proof does not use the Pythagorean Theorem and the Pythagorean Identity.

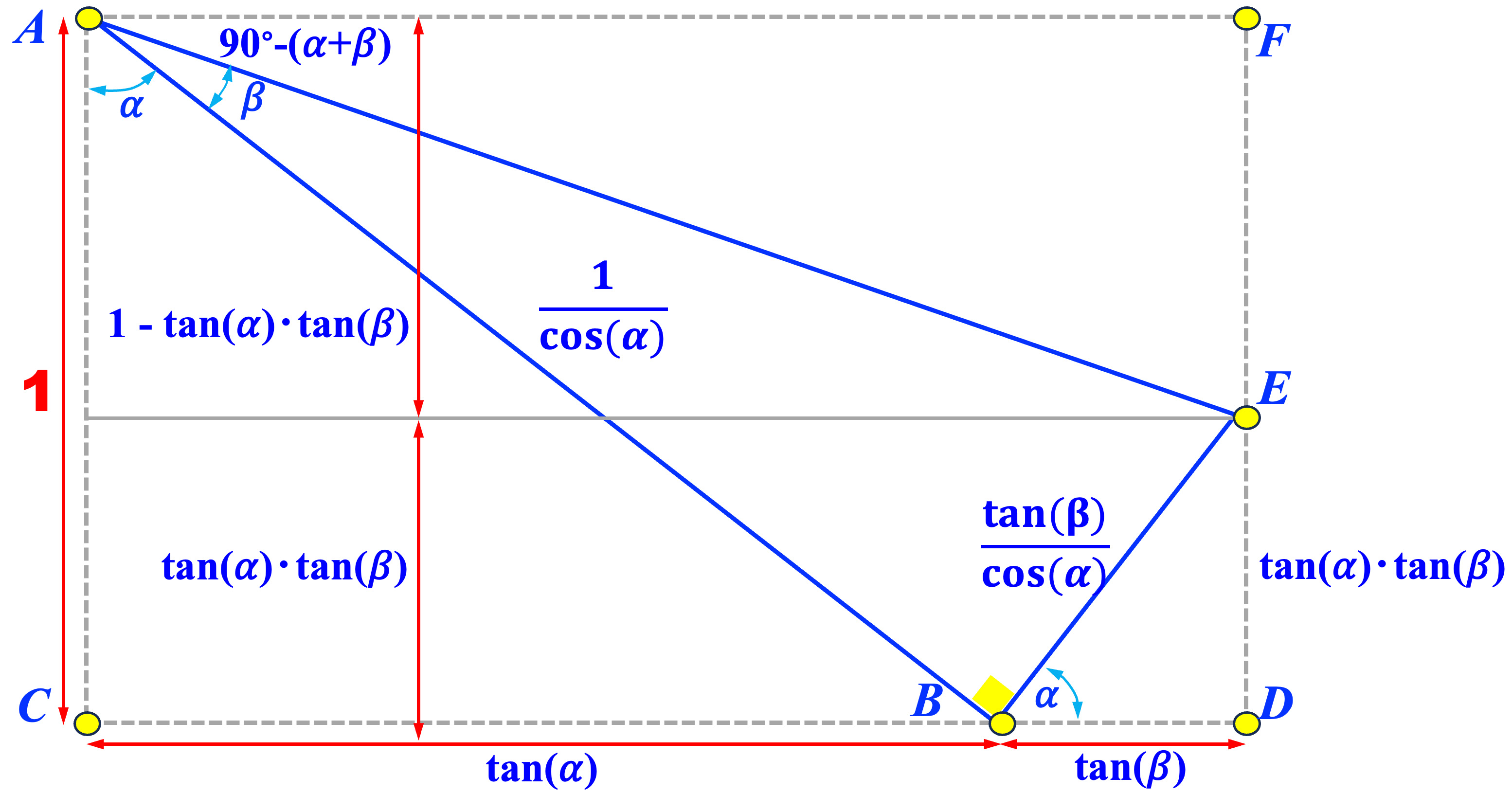
The right diagram above proves the angle sum identity for the tangent function. Let \( \bigtriangleup ABC \) be a right triangle with \( \angle C = 90^{\circ} \), \( \angle A = \alpha \) and \( \overline{AC} = 1 \). Then, we have \( \overline{BC}=\tan(\alpha) \) and \( \overline{AB} = \frac{1}{\cos(\alpha)} \). Let \( \bigtriangleup ABE \) be a right triangle with \( \angle ABE = 90^{\circ} \) and \( \angle BAE = \beta \). Then, \( \overline{BE}=\frac{\tan(\beta)}{\cos(\alpha)}\).

Let the perpendicular foot from \( E \) to \( \overleftrightarrow{BC} \) be \( D \) and the perpendicular foot from \( E \) to the line through \( A \) and parallel to \( \overleftrightarrow{BC} \) be \( F \). Therefore, \( ACDF \) is a rectangule. From \( \bigtriangleup DBE \) we have \( \overline{ED}=\tan(\alpha)\cdot\tan(\beta) \) and \( \overline{BD}=\tan(\beta) \). From \( \bigtriangleup EFA \) we have \( \overline{AF}=\overline{CD}=\tan(\alpha)+\tan(\beta) \) and \( \overline{EF}=1-\tan(\alpha)\cdot\tan(\beta) \). In this way, the angle sum identity for the tangent function is proved as follows: \[ \tan(\alpha+\beta) = \frac{1}{\cot(90^{\circ}-(\alpha+\beta))} = \frac{\overline{AF}}{\overline{EF}} = \frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\cdot\tan(\beta)} \]

In this way, we proved the angle difference and angle sum identities for the tangent function without using the Pythagorean Theorem and the Pythagorean Identity. All of these proofs appeared before Zimba's 2099 paper and Jackson-Johnson's 2023 work.

Lengvárszky

Go back to Home Page.