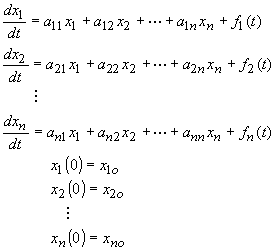
Given:
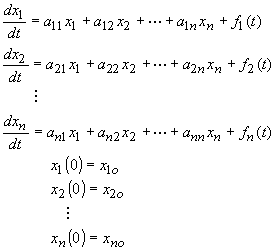
(The discussion will be limited to n=2. The method should generalize directly for n>2.)
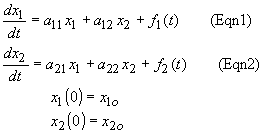
Method 1: Substitution methods
We need to reduce the problem to a higher order differential equation involving only either x1 or x2. First, take the derivative of both sides of (Eqn1), then substitute (Eqn2) for dx2/dt in the resulting equation:
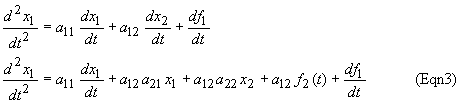
Next, solve for x2 in (Eqn1) and substitute this into (Eqn3),
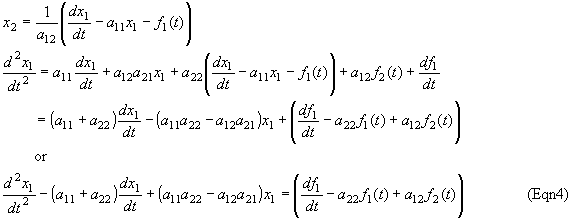
Note that (Eqn4) is now a second order linear ODE for x1 whose characteristic equation and eigenvalues are given by
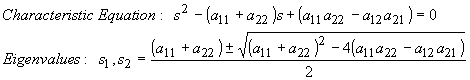
Once the complete solution for x1, containing two arbitrary constants, is found, it can be substituted into (Eqn1) to evaluate x2. The two initial conditions can then be used to determine the appropriate values for the two arbitrary constants.
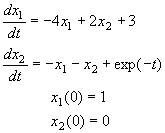
Following the method just proposed, we obtain
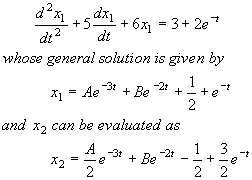
After applying the initial conditions, we find A=1 and B=-3/2
.
Method 2: Matrix Differential Operator Method
Denote the differential operator by D=d/dt, then (Eqn1) and (Eqn2) can be rewritten as
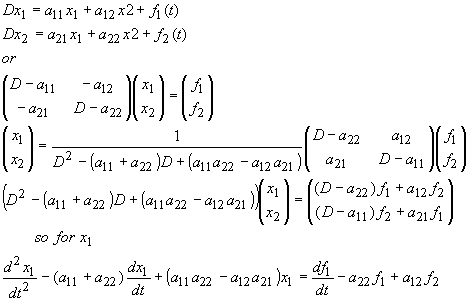
which is exactly (Eqn4) using the previous method.
Note that even though both methods gives the same high order differential equations the matrix differential operator method may be more convenient as n gets large.
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 1/14/2001.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295