Point Location
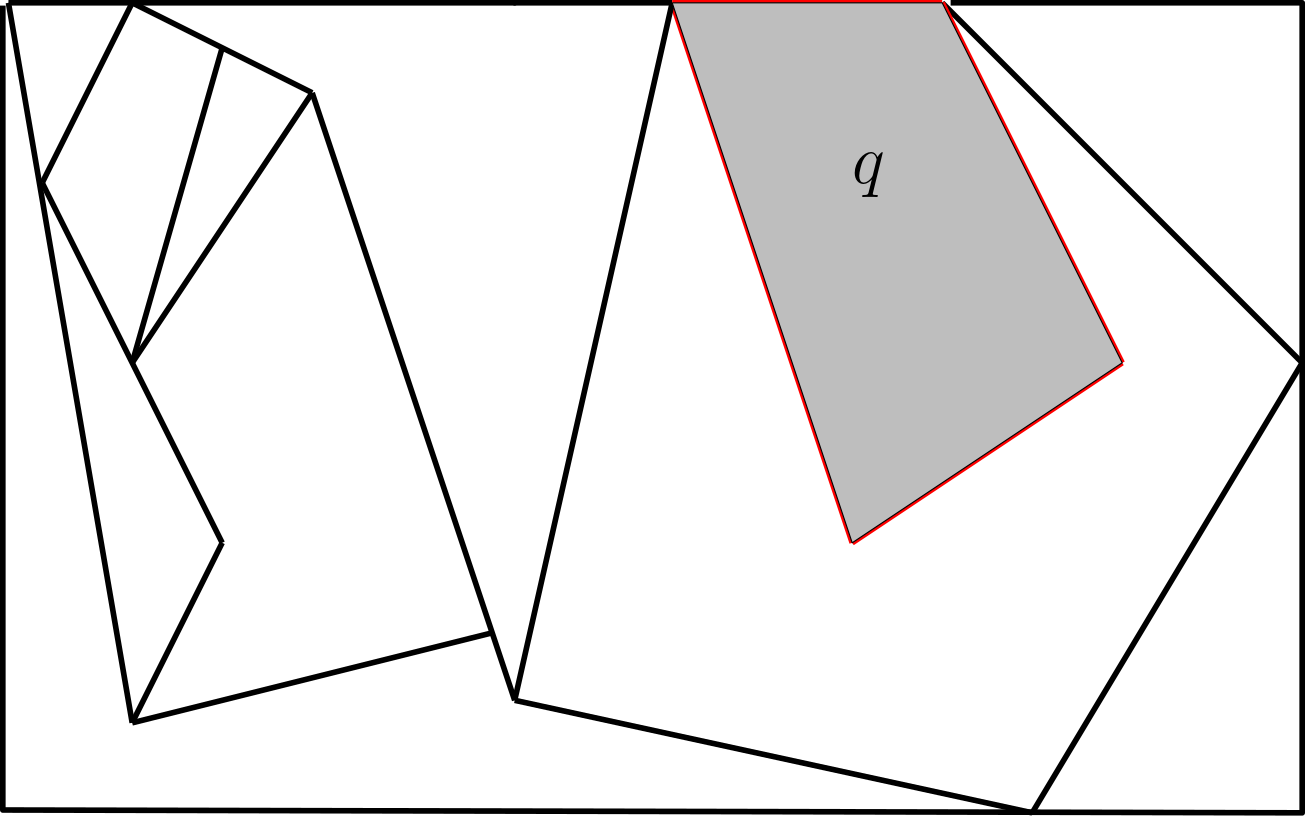
In the planar point location problem we store a polygonal subdivision of the plane in a data structure. For any query point q we must be able to find the polygon (also called the face) that contains q. The static data structure for this problem uses linear space and answers queries in O(log n) time. In the dynamic variant of this problem we must also support insertions and deletions of edges. Existence of a dynamic data structure with logarithmic time for both queries and updates has been an open question for several decades. A data structure with close to optimal trade-offs for this problem was constructed in 2015 (see Chan and Nekrich, SIAM J. Comp. 2018). Recently, this problem was completely resolved: there is a data structure that supports point location queries, insertions, and deletions in O(log n) time (see Nekrich, STOC 2021). A number of variants of the point location problem have also been studied extensively. Researchers considered e.g., point location in three dimensions, adaptive data structures, the case when the subdivision is not connected, and point location in the external memory model.
Publications
- T. M. Chan, Y. Nekrich
Towards an Optimal Method for Dynamic Planar Point Location
SIAM Journal on Computing (FOCS'15 special issue) [PDF]
- T. M. Chan, Y. Nekrich, S. Rahul, and K. Tsakalidis
Orthogonal Point Location and Rectangle Stabbing Queries in 3-d
45th International Colloquium on Automata, Languages, and Programming (ICALP 2018) [PDF] - J. I. Munro, Y. Nekrich
Dynamic Point Location in External Memory
35th International Symposium on Computational Geometry (SoCG 2019) [PDF] - Y. Nekrich
Optimal-Time Dynamic Planar Point Location in Connected Subdivisions
53rd ACM Symposium on Theory of Computing (STOC 2021) [PDF]
Orthogonal Range Searching
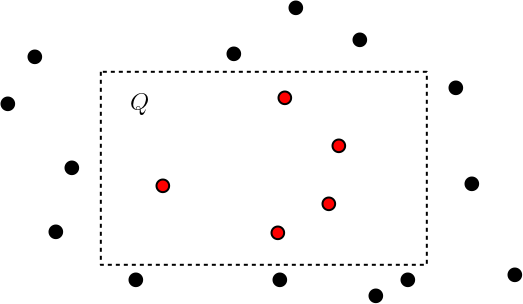
In this problem we keep a set of multi-dimensional points P in a data structure, so that for any axis-parallel query rectangle Q some information about points from P ∩ Q can be computed efficiently. Some frequently considered variants are range reporting (report the list of all points in P ∩ Q), range counting (compute the number of points in P ∩ Q), and range maxima (find the point with the highest priority in P ∩ Q). In addition to computational geometry, range searching is used in string algorithms and database theory.
Publications
- Y. Nekrich
New Data Structures for Orthogonal Range Reporting and Range Minima Queries
32nd ACM-SIAM Symposium on Discrete Algorithms (SODA 2021) [PDF] - Y. Nekrich
Four-Dimensional Dominance Range Reporting in Linear Space
36th International Symposium on Computational Geometry (SoCG 2020) [PDF] - T. M. Chan, Q. He, Y. Nekrich
Further Results on Colored Range Searching
36th International Symposium on Computational Geometry(SoCG 2020) [PDF] - T. M. Chan, Y. Nekrich
Better Data Structures for Colored Orthogonal Range Reporting
31st ACM-SIAM Symposium on Discrete Algorithms (SODA 2020) [PDF] - Y. Nekrich
Efficient Range Searching for Categorical and Plain Data
ACM Transactions on Database Systems (TODS) 39 (2014), PODS 2012 special issue [PDF]
Compressed Data Structures
Compressed data structures is a thriving research area at the intersection of data structures and data compression. The goal is to represent the data in the most compact way possible so that these data can be queried efficiently. The study of compressed data structures is motivated by the constantly growing volumes of data that must be stored and processed and by situations when the storage capacity is limited. Compressed data structures are interesting in their own right and as a part of algorithms that work on compressed data without decompressing it. Compressed data structures also find numerous applications in other areas, e.g., they are used to reduce the space consumption of geometric data structures. Although this area has been extensively studied for over two decades, there is still a number of important open questions.
Publications
- J. I. Munro, G. Navarro, Y. Nekrich
Space-Efficient Construction of Compressed Indexes in Deterministic Linear Time
27th ACM-SIAM Symposium on Discrete Algorithms (SODA 2017) [PDF] - J. I. Munro, Y. Nekrich
Compressed Data Structures for Dynamic Sequencess
23rd European Symposium on Algorithms (ESA 2015) [PDF] - J. I. Munro, Y. Nekrich, J. S. Vitter
Dynamic Data Structures for Document Collections and Graphs
34th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS 2015) [PDF] - G. Navarro, Y. Nekrich
Optimal Dynamic Sequence Representations
24th ACM-SIAM Symposium on Discrete Algorithms (SODA 2013) [PDF]