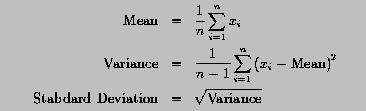
Computing and Printing the Input Data and Their Average: Version 5

WARNING: This example assumes spaces are ignored for the I and F descriptors and the output is sent to a printer.

Problem Statement

We shall rewrite a program discussed earlier. In this new version, report printing will take advantage of the slash edit descriptor to simplify the design of formats. Click here to review the earlier version.

The mean, variance and standard deviation of a set of data can be computed with the following formulas:

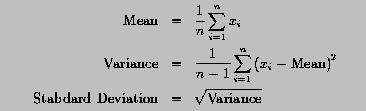
Write a program to read in a set of real values and use the above formulas to compute the mean, variance and standard deviation. Moreover, this program should generate a table containing the following addition information:

the input data,
the distance between the data to the mean, and
if a data is greater than the sum of mean and standard deviation, a mark Good should be displayed; if a data is less than mean - standard deviation, a mark Bad should be displayed.

The input data and the table should be printed as follows:

         1    1    2    2    3    3    4
....5....0....5....0....5....0....5....0
 Input Data:

  No  Data
 === ======
   1   6.60
   2   6.00
   3   4.00
     :
     :
     :
  10   5.20

 Mean               :       6.7100000
 Variance           :       3.3498888
 Standard Deviation :       1.8302702

 Analysis Table:

  No  Data    Dev
 === ======  =====
   1   6.60  -0.11
   2   6.00  -0.71
   3   4.00  -2.71 <-- Bad
   4   9.00   2.29 <-- Good
   5   4.50  -2.21 <-- Bad
   6   7.30   0.59
   7   9.50   2.79 <-- Good
   8   8.00   1.29
   9   7.00   0.29
  10   5.20  -1.51

Solution

! --------------------------------------------------------------------
! PROGRAM  MeanVariance:
!    This program reads in an array and computes the mean, variance
! and standard deviation of the data stored in the array.  Then, it
! displays an analysis table.  If a value is greater than the value
! of (mean + standard deviation), it displays a "good".  If a value
! is less than the value of (mean - standard deviation), it displays
! a "bad".
! --------------------------------------------------------------------

PROGRAM  MeanVariance
   IMPLICIT  NONE

   INTEGER, PARAMETER :: MAX_SIZE = 50       ! maximum array size
   REAL, DIMENSION(1:MAX_SIZE) :: Data       ! input array
   REAL               :: Mean, Variance, StdDev   ! results
   INTEGER            :: n                   ! actual array size
   INTEGER            :: i                   ! running index
   CHARACTER(LEN=40)  :: TitleHeading = '(1X, A//1X, A/1X, A)'
   CHARACTER(LEN=20)  :: For_Data     = '(I4, F7.2)'
   CHARACTER(LEN=50)  :: ResultFormat = '(/1X, A, F15.7/1X, A, F15.7/1X, A, F15.7/)'
   CHARACTER(LEN=20)  :: For_Analysis = '(I4, 2F7.2, A)'

   READ(*,*)  n                              ! read in input array
   READ(*,*)  (Data(i), i = 1, n)
   WRITE(*,TitleHeading)  "Input Data:", &
                          " No  Data",   &
                          "=== ======"
   WRITE(*,For_Data)   (i, Data(i), i = 1, n)

   Mean = 0.0                                ! compute mean
   DO i = 1, n
      Mean = Mean + Data(i)
   END DO
   Mean = Mean / n

   Variance = 0.0                            ! compute variance
   DO i = 1, n
      Variance = Variance + (Data(i) - Mean)**2
   END DO
   Variance = Variance / (n - 1)
   StdDev   = SQRT(Variance)                 ! compute standard deviation

   WRITE(*,ResultFormat)  "Mean               : ", Mean,      &
                          "Variance           : ", Variance,  &
                          "Standard Deviation : ", StdDev
   WRITE(*,TitleHeading)  "Analysis Table:",     &
                          " No  Data    Dev ",   &
                          "=== ======  ====="
   DO i = 1, n
      IF (Data(i) > Mean + StdDev) THEN
         WRITE(*,For_Analysis)  i, Data(i), Data(i) - Mean, " <-- Good"
      ELSE IF (Data(i) < Mean - StdDev) THEN
         WRITE(*,For_Analysis)  i, Data(i), Data(i) - Mean, " <-- Bad"
      ELSE
         WRITE(*,For_Analysis)  i, Data(i), Data(i) - Mean
      END IF
   END DO

END PROGRAM  MeanVariance

Click here to download this program.

Program Input and Output

If the input data consist of the following:

10
6.6  6.0  4.0  9.0
4.5  7.3  9.5  8.0
7.0  5.2

The output of the program is:

         1    1    2    2    3    3    4
....5....0....5....0....5....0....5....0
 Input Data:

  No  Data
 === ======
   1   6.60
   2   6.00
   3   4.00
   4   9.00
   5   4.50
   6   7.30
   7   9.50
   8   8.00
   9   7.00
  10   5.20

 Mean               :       6.7100000
 Variance           :       3.3498888
 Standard Deviation :       1.8302702

 Analysis Table:

  No  Data    Dev
 === ======  =====
   1   6.60  -0.11
   2   6.00  -0.71
   3   4.00  -2.71 <-- Bad
   4   9.00   2.29 <-- Good
   5   4.50  -2.21 <-- Bad
   6   7.30   0.59
   7   9.50   2.79 <-- Good
   8   8.00   1.29
   9   7.00   0.29
  10   5.20  -1.51

Discussion

We will not discuss the logic of this program. In what follows, only the output part will be addressed. Please click here for the details of program logic.

Two places can be improved. The first one is the report title and table heading.
```
         1    1    2    2    3    3    4
....5....0....5....0....5....0....5....0
 Input Data:

  No  Data
 === ======
```
The report title Input Data: and table headings No and Data can be incorporated into a single format.
```
CHARACTER(LEN=40)  :: TitleHeading = '(1X, A//1X, A/1X, A)'

WRITE(*,TitleHeading)  "Input Data:", &
                       " No  Data",   &
                       "=== ======"
```
As you can see, we just pull all formats together into a single one. The title Title Data: is printed with 1X,A. The blank line between the title and the table heading is generated by //. Then, both No Data and === ===== are printed with 1X,A.
Note that the second table shares the same structure with the first one. Here are the table headings:
```
         1    1    2    2    3    3    4
....5....0....5....0....5....0....5....0
 Input Data:

  No  Data
 === ======

 Analysis Table:

  No  Data    Dev
 === ======  =====
```
While the second table has three columns, the column heading is simply a CHARACTER string and as a result can be printed with 1X,A.
The second place that can be converted to use a single format is printing the mean, variance and standard deviation.
```
         1    1    2    2    3    3    4
....5....0....5....0....5....0....5....0

 Mean               :       6.7100000
 Variance           :       3.3498888
 Standard Deviation :       1.8302702
```
Each line has a format of A for printing the description followed by F15.7 for printing the result. Note that there is a blank line above and below these results and hence slashes are used. This is the following format and WRITE:
```
CHARACTER(LEN=50)  :: ResultFormat = '(/1X, A, F15.7/1X, A, F15.7/1X, A, F15.7/)'

WRITE(*,ResultFormat)  "Mean               : ", Mean,      &
                       "Variance           : ", Variance,  &
                       "Standard Deviation : ", StdDev
```
In this way, we do not even use WRITE(*,*) for generating blank lines! From this example, you should be able to see the power of the slash edit descriptor.