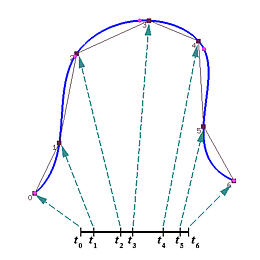
Parameter Selection Overview

The input to a B-spline interpolation/approximation algorithm usually consists of a set of data points. Thus, the first step is to find a set of parameters that can "fixed" these points at certain values. More precisely, if the data points are D₀, ..., D_n, then n+1 parameters t₀, ..., t_n in the domain of the curve must be found so that data point D_k corresponds to parameter t_k for k between 0 and n. This means that if C(u) is a curve that passes through all data points in the given order, then we have D_k = C(t_k) for all 0 <= k <= n. In the figure below, we have seven data points (i.e., n = 6) and seven parameters must be found to setup the desired correspondence.

There are infinite number of possibilities for selecting these parameters. For example, we can evenly divide the domain, or randomly pick n+1 values from the domain. However, poorly chosen parameters cause unpredictable results. The following figure shows four data points and three interpolating curves, each of which is obtained using a different set of parameters. One of them bends outward too much and creates an unnecessary bulge. The black curve has a peak and a small bulge. Only the one between these two follows the trend of data points closely. Thus, the choice of parameters affects the shape of the curve, and, consequently, affects the parameterization of the curve.

On the next few pages, we shall discuss a number of parameter selection methods, which include the Uniformly Spaced Method, Chord Length Method and Centripetal Method. Once a set of parameters is obtained, we need to compute a knot vector. See Knot Vector Generation for the details. We will also discuss the Universal Method in which a uniformly spaced knot vector is chosen and then used for computing the parameters. Please keep in mind that there are other methods for selecting parameters.