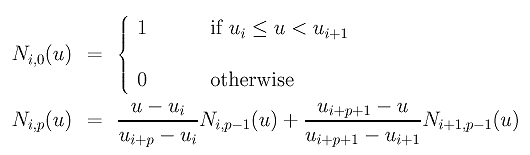

Although de Boor's algorithm is a standard way for computing the point on a B-spline curve that corresponds to a given u, we really need these coefficients in many cases (e.g., curve interpolation and approximation). We shall illustrate a simple way to do this.
Given a clamped B-spline curve of degree p defined by n+1 control points P0, P1, ..., Pn, and m+1 knots u0=u1=...=up=0, up+1, up+2, ..., um-p-1, um-p=um-p+1=...= um=1, we want to compute the coefficients N0,p(u), N1,p(u), ..., Nn,p(u) for any given u in [0,1]. A naive way is the use of the following recurrence relation:
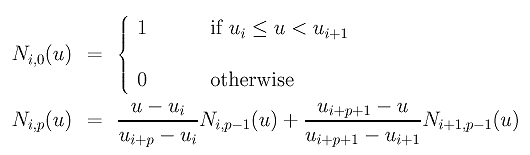
However, this is a very time consuming process. To compute Ni,p(u), we need to compute Ni,p-1(u) and Ni+1,p-1(u). To compute Ni,p-1(u), we need to compute Ni,p-2(u) and Ni+1,p-2(u). To compute Ni+1,p-1(u), we need Ni+1,p-2(u) and Ni+2,p-2(u). As you can see, Ni+1,p-2(u) appears twice, and, as a result, its recursive computations will also be repeated. As the recursion goes deeper, more duplicated computations will occur. This is very similar to the recursive version of de Casteljau's algorithm discussed on a previous page. Consequently, the computation speed is very slow.
There is an easy way. Suppose u is in knot span [uk,uk+1). An important property of B-spline basis functions states that at most p+1 basis functions of degree p are non-zero on [uk,uk+1), namely: Nk-p,p(u), Nk-p+1,p(u), Nk-p+2,p(u), ..., Nk-1,p(u), Nk,p(u). By definition, the only non-zero basis function of degree 0 on [uk,uk+1) is Nk,0(u). As a result, the coefficients can be computed from Nk,0(u) in a "fan-out" triangular form as shown below:
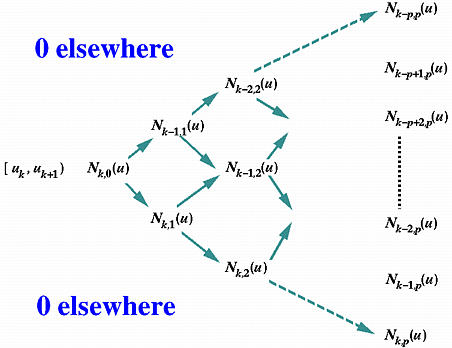
Since Nk,0(u) = 1 on knot span [uk,uk+1) and other B-spline basis functions of degree 0 are zero on [uk,uk+1), we can start from Nk,0(u) and compute the basis functions of degree 1 Nk-1,1(u) and Nk,1(u). From these two values, we can compute the basis functions of degree 2 Nk-2,2(u), Nk-1,2(u) and Nk,2(u). This process repeats until all p+1 non-zero coefficients are computed.
In this computation, "internal" values such as Nk-1,2(u) has a north-west predecessor (i.e., Nk-1,1(u)) and a south-west predecessor (i.e., Nk,1(u)); values on the north-east direction boundary of the above triangle such as Nk-1,1(u) has only a south-west predecessor (i.e., Nk,0(u)); and values on the south-east direction boundary of this triangle such as Nk,2(u) has only a north-west predecessor (i.e., Nk,1(u)). Thus, values that are on the north-east (resp., south-east) direction boundary use the second (resp., first) term of the recurrence relation in the definition. Only the internal values use both terms. Based on this observation, we have the following algorithm:
// now u is between u0 and um
Let u be in knot span
[uk,uk+1);
N[k] := 1.0 // degree 0 coefficient
for d :=1 to p do // degree d goes from 1 to p
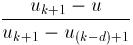 * N[(k-d)+1];
// right (south-west corner) term only
* N[(k-d)+1];
// right (south-west corner) term only 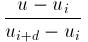 * N[i] +
* N[i] +
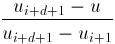 * N[i+1];
* N[i+1];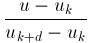 * N[k]; // let (north-west corner) term only
* N[k]; // let (north-west corner) term only Can you make this algorithm more efficient?