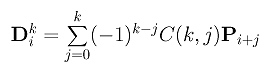

Before you proceed, please click here to review the concept and formulae of higher derivatives of a Bézier curve.
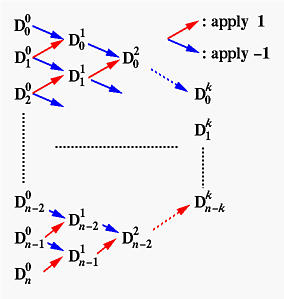
The control points of the k-th derivative curve of a Bézier curve of degree n are computed with the following diagram, were, point D0i is the control point Pi of the given curve, and points Dk0, Dk1, ..., Dkn-k are the control points of the k-th derivative curve. Note that the south-east (resp., north-east) bound arrows are associated with a multiplier of -1 (resp., 1).

How do we compute Dki, 0 <= i <= n-k, from the given control points? From an observation discussed on de Casteljau's algorithm page, we know that only control points Pi, Pi+1, ..., Pi+k will contribute to the computation of Dki. With the same technique used to prove the correctness of de Casteljau's algorithm, we have the following diagram:
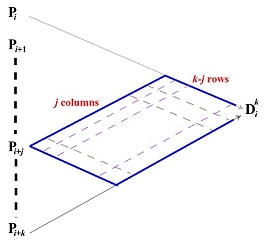
The contribution of Pi+j to the computation of Dki can only propagate to the intermediate points in the parallelogram as shown. This parallelogram has j "columns" and k-j "rows." Consequently, along each path from Pi+j to Dki the coefficient is (-1)k-j because there k-j (-1)'s and j 1's. Because there are C(k,j) such paths, the total contribution of Pi+j to the computation of Dki is (-1)k-jC(k,j). Therefore, we have