Half-Angle Identities for $ \sin() $ and $ \cos() $

Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created October 6, 2025

We all know the half-angle identities for $ \sin() $ and $ \cos() $ as follows: $$ \begin{eqnarray*} \sin\left( \frac{x}{2}\right) &=& \pm\sqrt{\frac{1-\cos(x)}{2}} \\ \cos\left( \frac{x}{2}\right) &=& \pm\sqrt{\frac{1+\cos(x)}{2}} \end{eqnarray*} $$ We shall prove these identities without using the Pythagorean Identity. Most materials on this page will be repeated in Luzia's 2015 Proof.

Consider a unit circle with center $ O $. Let $ \overleftrightarrow{OC} $ and $ \overleftrightarrow{OA} $ make an angle of $ x $, where $ A $ and $ C $ are on the circle and $ \overleftrightarrow{OC} $ is the x-axis. Without loss of generality, we assume $ 0 \leq x \leq 90^{\circ} $. Let $ E $ be the mid-point of $ \overline{AC} $. Let $ \varphi = \angle ACO $. From right triangle $ \bigtriangleup OCE $ we have $ \varphi = 90^{\circ} - \frac{x}{2} $ and hence $ \sin(\varphi) = \cos\left(\frac{x}{2}\right)$, $ \cos(\varphi) = \sin\left(\frac{x}{2}\right) $ and $ \overline{EC} = \sin\left( \frac{x}{2}\right) $. Therefore, $ \overline{AC}=2\overline{EC}=2\sin\left(\frac{x}{2}\right) $. From right triangle $ \bigtriangleup AOB $ we have $ \overline{OB} = \cos(x) $ and $ \overline{BC} = 1 - \cos(x) $. From right triangle $ \bigtriangleup ACB $ we have \[ \overline{BC}=\overline{AC}\cos(\varphi) =\overline{AC}\sin\left(\frac{x}{2}\right) = 2\sin^2\left(\frac{x}{2} \right) \] Because we have \[ 1-\cos(x) = \overline{BC} = 2\sin^2\left( \frac{x}{2}\right) \] rearranging yields the half-angle identity for $ \sin() $: \[ \sin^2\left( \frac{x}{2} \right) = \frac{1-\cos(x)}{2} \mbox{\ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ } \sin\left(\frac{x}{2}\right) = \pm\sqrt{\frac{1-\cos(x)}{2}} \]

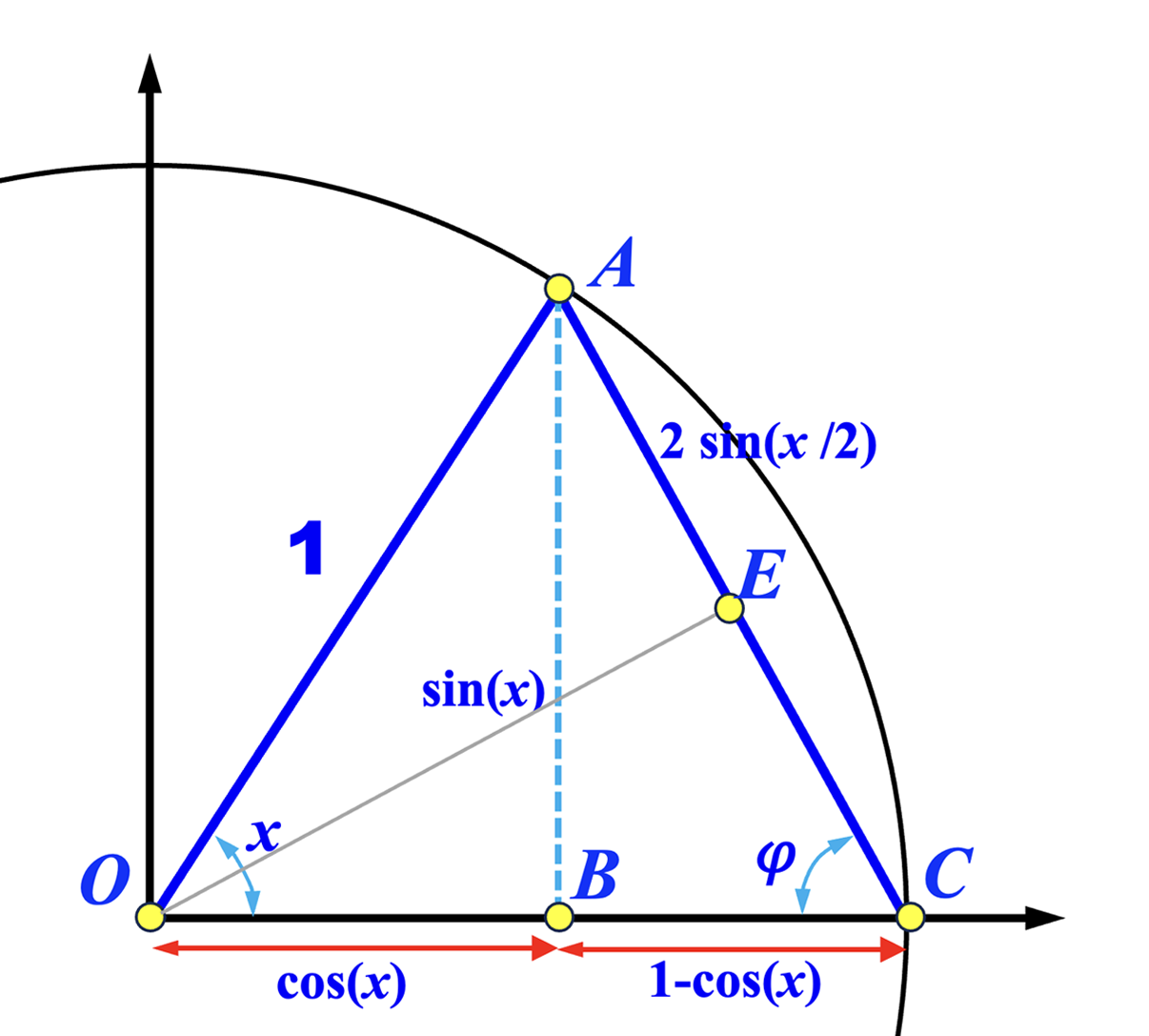
We have seen the double angle identities double angle identities for $ \cos(x) $: \[ \cos(x) = \cos^2\left( \frac{x}{2} \right) - \sin^2\left( \frac{x}{2} \right) \] Plugging in the $ \sin^2(x/2) $ obtained earlier, rearranging and simplifying yields: \[ \cos^2\left( \frac{x}{2} \right) = \frac{1+\cos(x)}{2} \mbox{\ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ } \cos\left(\frac{x}{2}\right) = \pm\sqrt{\frac{1+\cos(x)}{2}} \]
Neither the Pythagorean Theorem nor the Pythagorean Identity was used in deriving the half-angle identities. Therefore, the half-angle identities are independent of the Pythagorean Theorem and the Pythagorean Identity.
A quick note is necessary: from the identities for $ \sin^2(x/2) $ and $ \cos^2(x/2) $ the Pythagorean Identity is obvious. Moreover, due the symmetry and periodicity of $ \sin() $ and $ \cos() $, it is EASY to obtain the same results for any $ x $.
Go back to Home Page.

Half-Angle Identities for \( \sin() \) and \( \cos() \)