Is Proving the Pythagorean Identity a Conspiracy Theory?
Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created October 15, 2025
![]()
Ching-Kuang Shene (冼鏡光), Professor Emeritus
Department of Computer Science
Michigan Technological University
Houghton, MI 49931
USA
Created October 15, 2025
![]()
Let us start this page with two quotes from the previous page The Origin of the "Impossible" Proof Claim
| Your content seems to just be some conspiracy-theory-type ramblings about why the proof doesn't work. |
Here is the second one:
| Loomis's assertion is correct that the usual order of presentation of the material in mathematics has it such that the Pythagorean theorem is an ingredient in Trigonometry. That means that Loomis is correct that proofs of Pythagorean theorem using Trigonometry constituted circular reasoning, provided that one is using the usual mathematics. The students were also correct by avoiding the usual presentation order. That was all there was to the controversy. Your website fails to even cover the topic, just a lot of rambling. |
Two well-known trigonometry textbooks published in the 19th century will be used as an example, showing that the ways fo deriving the angle difference and angle sum identities without using the Pythagorean Theorem was a common way in trigonometry textbooks. Both 19th century textbooks are available online so that you can download copyes of them in various editions.
The first trigonomety textbook is Augustus de Morgan's 1849 Trigonometry and Double Algebra (image below).

|
On pp. 22-23, de Morgan proved the angle sum identity for \( \cos() \) near the end of page 23 using projection. This is exactly the same as the Coordinate Axes Rotation concept to be discussed later. Check the diagram on page 23 and you will understand the reason.

|
There are multiple copies of Ernest William Hobson's well-known book A Treatise on Plane Trigonometry on the web from the first edition in 1891 to some later editions. Here the 1897 second edition is used exclusively (left image below).

|
|
During that period and the first half of the 20th century, a popular topic in elementary geometry and trigonometry was the Fundamental Property of Projections, which is stated as follows:
|
The sum of the projections on any fixed straight line of the parts of any broken line joining two points \( P \) and \( Q \), depends only upon the positions of \( P \) and \( Q \), being independent of the manner in which \( P \) and \( Q \) are joined. |
The projection of a line segment \( \overline{PQ} \) on a straight line \( \overleftrightarrow{AB} \) is \( \pm \overline{PQ}\cdot\cos(\theta) \), where \( \theta \) is the angle between \( \overleftrightarrow{PQ} \) and \( \overleftrightarrow{AB} \) and \( \pm \) sign depends on the predetermined diredction of \( \overline{PQ} \). This property is, of course, independcent of the Pythagorean Theorem and the Pythagorean Identity. On p. 36 of Hobson's book, he used this property to prove the angle sum identities for \( \cos() \) and \( \sin() \) (right image above). This is the reason for Versluys to state in his 1914 book In trigonometry, it is usually shown without the aid of the Pythagorean theorem that \( \sin(B+C) = \sin(B)\cos(C) + \cos(B)\sin(C) \). Please see J. Versluys' 1914 Book for more details.
The following diagram is taken from Hobson's book on the fundamental property of projection. Note that all vertical lines should be perpendicular to \( \overleftrightarrow{AB} \). It basically says that if points \( P \) and \( Q \) be joined by any broken line, such as \( PpqrQ \), the sum of the projections of \( \overline{Pp} \), \( \overline{pq} \), \( \overline{qr} \), \( \overline{rQ} \) on \( \overleftrightarrow{AB} \), is equal to the projection of \( \overline{PQ} \) on \( \overleftrightarrow{AB} \). In many textbooks on trigonometry and analytic geometry this property was used to prove the angle difference and angle sum identities for \( \sin() \) and \( \cos() \).
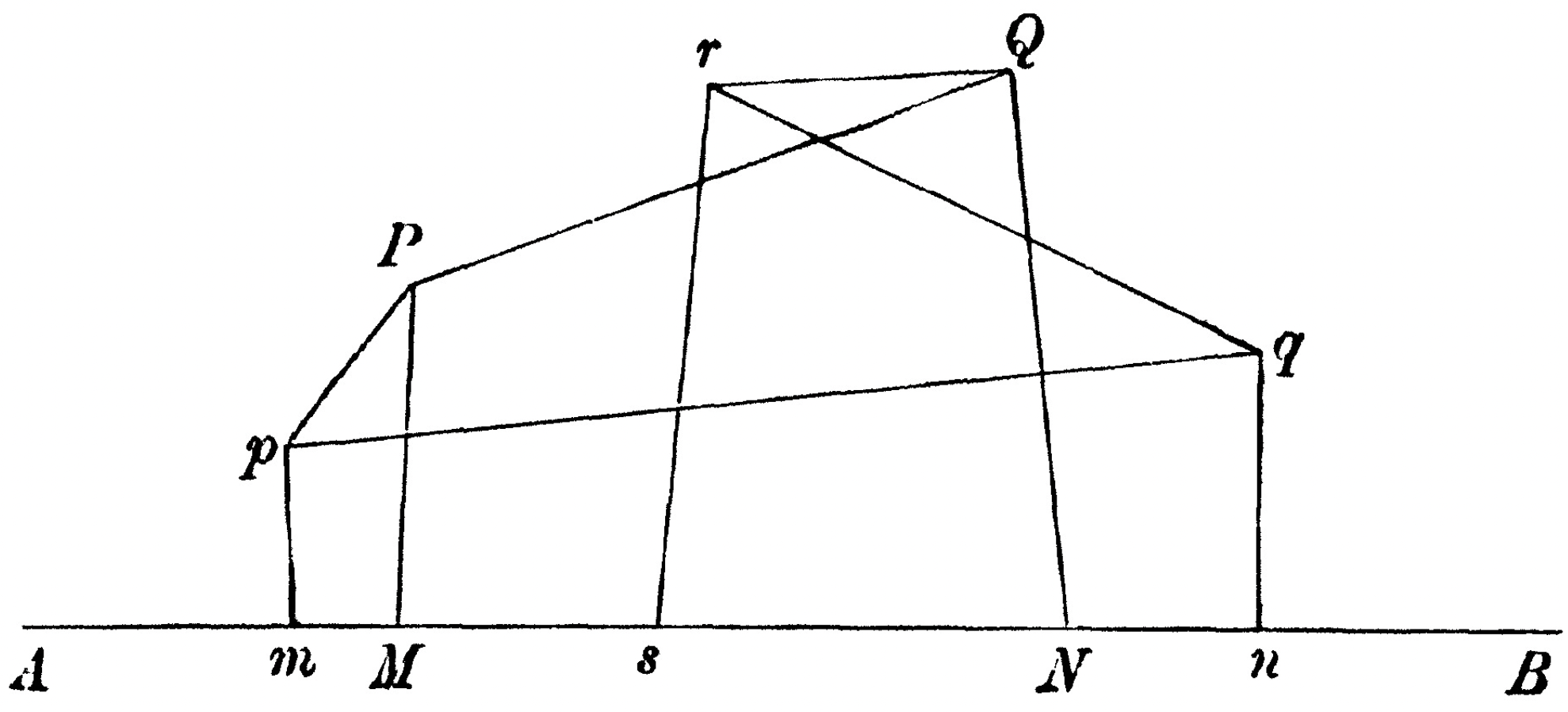
|
Then, let us move to the second quote.
| Loomis's assertion is correct that the usual order of presentation of the material in mathematics has it such that the Pythagorean theorem is an ingredient in Trigonometry. That means that Loomis is correct that proofs of Pythagorean theorem using Trigonometry constituted circular reasoning, provided that one is using the usual mathematics. The students were also correct by avoiding the usual presentation order. That was all there was to the controversy. Your website fails to even cover the topic, just a lot of rambling. |
First of all, you may find a PDF copy of Loomis' The Pythagorean Proposition here, which is a scan copy of the 1940 second edition. This copy is provided by US Department of Education. Page vii of this book stated the object of his work (the image below). Clearly, Loomis' book is a collection of what was known about the Pythagorean Theorem up to the late 1930s. No "usual" order of presentation of the materials in mathematics was involved. In other words, the "usual" order of presentation of mathematics was not something in his mind, because he treated the Pythagorean theorem as something "gobal" without considering a particular sequence of presentation. Consequently, treating the Pythagorean Theorem as part of a presenbtation sequence in which the Pythagorean Theorem is true is not an objective in Loomis' book. Furthermore, this book is for future investigator, who may not be the students learning geometry/trigonometry using a particular presentation sequence. It is even more important that there were at least TWO sequences even in the second half of the 19th century: one establishing the Pythagorean Identity using the Pythagorean Theorem and the other being the opposite. We have seen this on the current page and other pages at this site.

|
The Pythagorean Theorem and the Pythagorean Identity perhaps should be known to everyone who had gone through high school education. Why am I supposed to repeat this very basic knowledge here to consume more web resources.
The following is a screenshot from Loomis' book p. 244 on which Loomis stated NO TRIGONOMETRIC PROOFS. Please read it carefully. It also appeared on the Impossible Proof page. I just reproduce it here for your convenience.

It is very clear that Loomis' claim NO TRIGONOMETRIC PROOFS is universal without any quantifier. In other words, Loomis seemed to believe that the CAN ONLY option discussed on the previous page holds unconditionally. As a result, he stated Trigonometry IS because the Pythagorean Theorem IS. This also means that because of the existence of the Pythagorean Theorem, we have trigonometry.
Let me remind you again. Loomis' book is a collection of proofs of the Pythagorean Theorem and is independent of any "presentation order." We also showed two well-known textbooks published in the 19th century, one by de Morgan in 1849 and the other one by Hobson in 1891 (first edition). Both approached the angle sum and angle difference identities for \( \sin() \) and \( \cos() \) without using the Pythagorean Theorem and the Pythagorean Identity. From the angle sum and angle difference identities, the Pythagorean Identity can be easily proved. If the approach by de Morgan and Hobson is the "usual" way, then some later approaches using the Pythagorean Theorem to establish the Pythagorean Identity becomes obviously "unusual."
In summary, there is only a unified mathematics and there is no "usual" or "usususal" mathematics. The argument of usual order of presentation is perhaps an excuse rather than a good reasoning. Of course, studying whether the Pythagorean Theorem or the Pythagorean Identity can be proved by trigonometry is not a conspiracy type rambling. Instead, it is a legitimate way of doing methmatics.
Go back to Home Page.