什麼是焦距？

什麼是焦距？

冼鏡光
January 28, 2009上線
December 29, 2024搬家到此

在看這篇文章之前，建議您先看看從透鏡說起這篇文章。

選擇鏡頭時第一個考量的重要因素恐怕是鏡頭的焦距，第二項也許就是光圈。 不過相機鏡頭少則三五片透鏡、多則十餘片，如此複雜的相機鏡頭的焦距從何而來？ 物理學教科書中的焦距通常只用單透鏡說明，這個單透鏡理論又如何用到複雜的相機鏡頭上呢？ 這篇文字嚐試在動用最少數學與物理學觀念的前提下，為您一步一步地用直覺的方式解釋這個論題。

徹底了解焦距的觀念是很重要的，因為和鏡頭有關的資訊與討論總是離不開焦距， 而且很多重要概念（譬如f值、視角等等）都直接使用焦距。 所以正本清源，在談其它相機鏡頭的課題之前，我們得把焦距的基本觀念好好說一說。

焦距 -- 直覺的定義

透鏡大致上分成凸透鏡與凹透鏡兩類，我們先看凸透鏡，放大鏡就是個典型的凸透鏡。 找一個睛天出太陽的日子，拿一個放大鏡到戶外水泥地或磚牆邊，然後把放大鏡對正太陽前後移動， 就會發現地上或牆上有個很亮的點，這就是太陽透過放大鏡所得到的像。 在前後移動放大鏡（相當於對焦）時太陽的像會改變大小，把放大鏡移到使太陽的像最小也最亮的位置（對焦成功）， 於是從太陽的像到放大鏡中心點的距離就是放大鏡的焦距（focal length）、也叫做焦長，太陽的像所在位置是放大鏡的焦點（focal point）。 如果在原位置把放大鏡反過一面對正太陽，也會發現焦距與原來的幾乎一樣。

因為太陽的位置離放大鏡太遠，我們不妨想像成是在無限遠處； 又因為放大鏡對正太陽，這等於是說太陽是在放大鏡軸線（經過放大鏡中心並且與放大鏡垂直的直線）上無限遠的地方。 從無限遠出發、沿軸線方向前進的入射光可以看成是一束平行線，只要想想鐵路雙軌永遠平行、 但我們總是有一個它們會在很遠很遠處相交的感覺（這是透視效果），於是就不難理解上面的說法。 所以，從軸線上無窮遠處的物體（太陽）出發、依軸線方向自左而右進行的光線（入射光）正是與軸線平行的線條（見下圖）， 這些光線經過凸透鏡折射後會在軸線上某個點匯聚，這個點是凸透鏡的焦點，從焦點到放大鏡中心的距離是焦距。 綜合起來，我們有這樣的定義：給了一個非常薄、薄到厚度可以略而不計的凸透鏡L（用兩個向外指的箭頭表示、見下圖）， 與透鏡軸線平行（自左而右）的入射光經過透鏡折射後會在軸線上某個點匯聚，這個點是該凸透鏡的焦點， 從焦點到透鏡中心的距離是焦距；另外，自右而左與軸線平行的入射光定出在凸透鏡的另一側焦點。

任何一個在無限遠的點都可以經過透鏡成像。 從一個在無限遠的點出發、以某個方向到達透鏡的入射光也可以視為沿同一個方向的平行線（見上圖）， 它們到達透鏡後會被折射、再匯聚成一點，這個點是該無限遠點經個透鏡得來的像（見圖中黄色方格）。 空間中所有在無限遠的點可以想像成在一個無限遠平面（plane at infinity）上，它們經過透鏡的像當然也在一個平面上， 而且這個平面包含了焦點，因為焦點是沿軸線方向在無限遠點的像。 所以，包含所有在無限遠點的像的平面與軸線垂直、而且經過焦點， 這個平面叫做焦平面（focal plane），這是上圖中的F； 因為透鏡有兩個焦點，所以有兩個焦平面。 歸結起來，焦平面包含了所有在無限遠的點的像，它到透鏡的距離等於焦距。

再看凹透鏡的情形，下圖中L是一個非常薄、薄到厚度可以不計的凹透鏡，我們用兩個箭尾表示。 從無限遠出發並且與軸線平行（自左而右）的入射光到達凹透鏡L之後會被折射， 與凸透鏡不同的是，在凹透鏡下穿過透鏡的光會散開（亦即發散），不過這些光線的延長線會在軸線上交於一點， 這是凹透鏡的焦點（但在透鏡的左邊），從焦點到透鏡中心的距離是焦距。

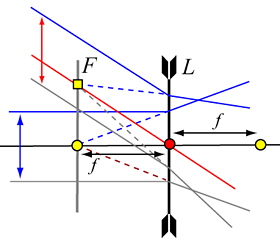
再考慮一個不在軸線上的無限遠點，從那兒出發以某個方向進行的入射光就是與該方向平行的光束， 它們到達透鏡L時也會散開，因為這些光線來自在無限遠的同一點，它們的延長線也會交於一點（圖中的黄色方格）。 與凸透鏡相同的是，所有在無限遠的點可以看成是在一個平面上，於是所有無限遠點的像也在一個平面上， 這個平面（亦即焦平面F）與凹透鏡的軸垂直而且經過焦點。 與凸透鏡不同的是，這些像是光線延長線的交點、並不在實際光路上，所以都是虛像； 另外，凸透鏡的實像在透鏡右邊，但凹透鏡的虛像在透鏡的左邊。

讓我們把上面的討論做個整理。不論是凸透鏡還是凹透鏡，從無限遠出發沿某個方向自左而右到達透鏡的平行入射光經折射後， 這些光線或它們的延長線會交於一點（在無限遠點的像）； 所有無限遠點的像都在焦平面上，焦平面與軸線的交點是焦點，從焦點到透鏡中心的距離是焦距。 要注意的是，在凸透鏡下，一個無限遠點的像在透鏡右側，是個實像；但在凹透鏡下，無限遠點的像在透鏡左側，是個虛像。 很重要的是，到目前為止我們都假設透鏡是薄的、薄到厚度可以不計，因此用線段加上箭頭（凸）或箭尾（凹）表示， 不過我們稍後也會講到如何引入透鏡厚度的方法。 要再次提醒的是，焦點與焦距的定義來自從軸線上無限遠出發、與軸線平行的光線。

接下來的幾節從這個基本結構開始，講解薄透鏡原理、再擴充到厚透鏡，然後討論複透鏡，最後看幾個實際的相機鏡頭做結束。 為了避免引入太多數學內容，我們假設入射光都很靠近透鏡的軸線（近軸光學），於是整個討論就大為化簡， 而且與高中或大學物理教科書的材料一致。

成像原理 -- 直射光

單片薄透鏡的成像原理是基於三絛特殊光線中的任何兩條，我們先從凸透鏡談起。 下圖中這三條光線用藍色、紅色、灰色表示，圖中透鏡左邊有一個高為O（物長）的被攝體， 它到透鏡的距離為u（物距），透鏡有兩個焦點（圖中的黃點），焦距為f。 第一道光線（藍色）從被攝體頂點（淺藍方形）出發、與鏡頭軸線平行，到達透鏡後被折射向右邊焦點前進； 第二道光線（紅色）穿過透鏡中心沒有折射； 第三道光線穿過左邊的焦點，到達透鏡被折射後與透鏡軸線平行。 因為這三道光線都是從被攝體頂點出發，經過折射後當然會交於一點，這是被攝體頂點的像。 因為三道光線交於一點，從被攝體頂點出發，任取兩道就可以求出它的像。 我們用v表示像到透鏡的距離（像距），並且用I表示被攝體的像的長度（像長）， 於是m = I/O就是放大率（像長比物長）。

用幾何學的相似三角形觀念，從上圖不難導出O、I、u、v、 f這幾個值滿足下面三道重要式子； 第一是透鏡公式：

第二是牛頓（Newton）公式：

從透鏡公式與放大率公式可以看出： （1）當物距u趨近無限大（被攝體在無窮遠）時， 1/u趨近於0，於是像距v趨近於f、放大率m趨近於0； （2）當物距u趨近於焦距時，像距v趨近於無限大， 放大率m也趨近於無限大。

再看凹透鏡的情形（見下圖）。 從被攝體頂點出發而且與透鏡軸線平行的光（藍色）到達透鏡後，會被折射散開，但它的延長線（虛線）會經過左邊的焦點。 第二條光線（紅色）通過鏡頭中心，不會被折射。 第三條光線（灰色）的延長線會經過右邊的焦點，但到達透鏡時會被折射變成與透鏡軸線平行， 向後延伸（虛線）與第一道光線的延長線以及第二道光線交在一點，這是被攝體頂點的像。 因為這個像是由虛（延長）線得來，所以凹透鏡得到虛像。

如果仍然用O、I、u、v、f表示物長、像長、物距、像距、焦距， 使用相似三角形的觀念也可以導出三道基本式子。 第一道是透鏡公式：

第二道是牛頓公式：

第三道是放大率公式：

比較凸透鏡與凹透鏡對應的式子，就會發現它們十分相似，通常只差個正負號。 為什麼會有正負號的差異呢？根本的問題在於凸透鏡讓（從左邊來的）光線經過透鏡右邊的焦點、 而且像在透鏡右邊（至少圖是這樣畫的，但卻不一定永遠如此，見下文）， 但在凹透鏡時光線的延長線卻經過透鏡左邊的焦點、而且虛像在透鏡的左邊，這個左右的差異造成正負號的差異。

為了讓兩組式子一致，光學教科學通常會引進某種慣例，此地使用以下幾點：

  1. 入射光從左邊進入鏡頭，於是u是正；
  2. 如果匯聚的焦點在透鏡的右（或左）邊，f是正（或負）值；
  3. 若像在透鏡的右（或左）邊，v是正（或負）值；
  4. 如果入射光從右邊進入透鏡，u、v與f都變號。
我們回頭看凹透鏡的情形，因為用左邊的焦點而且像也在左邊，所以f與v都用負值， 因此在透鏡公式與牛頓公式中都得用-f與-v。 把這兩式稍做整理、使v與f都帶負號，就會得到：

於是凹透鏡的兩道式子與對應的凸透鏡式子就完全相容了。 因為放大率恆為正值，在凹透鏡情況得用絕對值。

有了這個觀念之後我們不妨做幾個簡單的推論。

  1. 在透鏡公式中，如果被攝體到凸透鏡的距離（物距u）小於焦距f， 於是1/v = 1/f - 1/u小於零， 這表示像距v小於0，被攝體的像出現在凸透鏡的左邊，它是個虛像、不會在底片或感光晶片上成像。 下圖是個例子，在那兒u = 1而f = 2，解出v = -2。
  2. 在凸透鏡情況下，如果物距u大於焦距f（亦即被攝體在焦點左邊），於是v大於0、 像在凸透鏡右邊而且可以在底片或感光晶片上成像。
  3. 從凸透鏡成像的圖與上一點，如果物距大於焦距（亦即u f）， 那麼像距也會大於焦距（亦即v > f）； 所以在有實像的情況下，像永遠在焦點的右邊。
  4. 再看凹透鏡，從透鏡公式可知1/v = 1/(-f) - 1/u永遠小於0， 於是像距為負值、像在凹透鏡的左方，因此不可能在底片或感光晶片上成像。

成像原理 -- 斜射光

上一節談到三道特殊光線與它們到達透鏡後被折射的情形，那麼任意的光線是如何折射的呢？ 這是個看起來不很容易，但事實上卻不十分難的問題。

下圖中藍色表示一道任意的入射光，我們想要知道它到達透鏡後的折射方式。 回想一下焦點的定義，它是在軸線上無窮遠處一個點的像，於是在無限遠平面上的每一個點的像就都在經過焦點、 並且與軸線垂直的平面（叫做焦平面、focal plane）上。 我們可以把藍色的光想像成是從無限遠平面上某個點出發、以藍色線條方向進行的光線，與上一節一樣， 從同一個在無限遠的點出發而與藍色光線同一方向的光線中會有一條經過透鏡中心（紅色）、也會有一條經過透鏡的焦點（灰色）； 在這二者中，紅色光線不會折射，灰色光線到達透鏡後會折射成與軸線平行。 因為這三道光線來自同一點，它們會交在同一點；因為原來的點在無限遠，它的像在焦平面上。

有了這個基本概念之後，用下面幾步就可以作出入射光的折射方向（見下圖）：

  1. 令入射光（藍色）與透鏡的交點為A，
  2. 從焦點作一條與入射光平行的線（灰色）、與透鏡交於B，
  3. 經過B作一條與軸線平行的直線， 令它和經過另一個焦點而且與軸線垂直的線交於C，
  4. 連結A與C的直線就是入射光折射後的結果。

這個手法也可以用來求出軸線上任何一點P的像Q，我們只要從P任作一條（下圖的藍色）光線， 假設它與透鏡在A處相交，然後依上述的方式作圖找出折射的方向， 這條折射光或它的延長線與軸的交點Q就是P的像。

厚透鏡

講完薄透鏡之後就應該說厚透鏡了，以下只用凸透鏡說明，您不難用前面的觀念改成為凹透鏡。 下面的圖是一個厚凸透鏡L，我們仍然用藍、紅、灰三道光線做說明。 首先，從P出發的藍色與軸線平行的入射光到達透鏡L的表面時會折射進入透鏡， 到達透鏡第二個表面會再度折射離開透鏡，並且與軸線在F2相交； 因為入射光與軸線平行，折射後會經過焦點，所以F2是兩個焦點之一， 當然P的像Q會在這道（出射）光上某處。 反過來，從Q出發的灰色與軸線平行的入射光到達透鏡L的表面時會折射進入透鏡， 到達第二個表面會再度折射離開透鏡，並且與軸線在F1相交、再到達P，

再回頭看藍色的光線，與軸平行的入射光延長線（虛線）以及到達焦點F2的出射光延長線會在某處相交。 不但如此，因為每一條與軸平行的入射光都會折到焦點F2， 於是平行部份與到達F2的出射光延長線也會交在一點，所有的這些點構成一個曲面， 但因為只考慮離軸很近的光線，這個曲面差不多就是個平面， 我們把這個平面叫做主平面（principle plane）、 簡稱做主面。 同樣的道理，從Q出發而且與軸平行的（灰色）光線經過折射後會經過焦點F1而到達P， 於是入射光與到達F1的出射光交點也定義了另一個主面。

有了主（平）面之後，透鏡內折射的手續就可以省略了，因為進入鏡頭並且與軸線平行的光線可以想像成直線進行， 到達主面後再折射到對應的焦點，所以厚透鏡的折射關係可以用兩個主面表示、使折射的討論簡化成只比薄透鏡稍許複雜一點； 當然，若兩個主面重合，這個厚透鏡就變成一個薄透鏡。

此外，不論是那一個方向的入射光，都會有一道光線進入鏡頭與離開鏡頭的方向相同（亦即平行）， 這相當於薄透鏡中經過透鏡中心的光線，也是上圖中的紅線。 把這道特殊的入射光延長（圖中紅色虛線）與軸線交於一點Ｎ2， 把出射光部份向後延伸也與軸線有一個交點Ｎ2， 這兩個點叫做，節點（nodal point）， 經過節點而與軸線垂直的平面叫做節面（nodal plane）。

如果透鏡兩側的介質相同（譬如在一般拍攝時介質就是空氣），主面與節面重合，主面與軸線的交點就是節點（見上圖）。 但若透鏡兩側的介質不同（譬如水下攝影時入射光側是水、出射光側是空氣），主面與節面不同，當然節點位置也不同。 以下為了方便起見，我們假設透鏡兩邊的介質相同，因此主面與節面重合，整個討論會大為化簡。

焦點與節點的對應是十分重要的。 從左邊來與軸線平行的入射光到達N2的節面時會折射到焦點F2， 從右邊來與軸線平行的入射光到達N1的節面時會折射到焦點F1， 所以F1與N1一組，F2與N2是另一組。

正因為有了兩個節面，物距、像距、與焦距的定義就有點不同了。 首先，焦距f是從某個焦點到與它對應節點的距離； 同樣地，物距u與像距v都是到對應節點的距離，請看上圖。 在這樣的定義下，透鏡公式、牛頓公式、與放大率公式都成立而不必更動。

複透鏡

絕大多數的相機鏡頭都不只一片透鏡，使用前面提過的成像原理，我們可以把鏡頭的焦點、節點與焦距找出來，於是鏡頭的基本特性就有了。 為了方便說明，我們假設所有透鏡都是薄透鏡，這是個合理的假設，因為厚透鏡可以轉換成焦點、節點與節面， 於是成像原理就與薄透鏡相同，唯一差異是多了兩個節面之間的距離。

如果我們知道鏡頭中每一片透鏡的位置與焦點，找出鏡頭焦點與節點的手續有兩個步驟： （1）從左方產生一道與軸線平行的入射光，使用成像原理讓這道光穿過每一片透鏡， 最後出射光與軸線在某處相交，這就是右邊的焦點F2； （2）把入射光與經過F2的出射光延長，它們會在某處相交， 從這個點向軸線作垂直線（節面）交於N2， 這就是與F2對應的節點， 因此F2與N2間的距離是焦距f。 接著從右邊產生一道與軸線平行的入射光，用同樣手續可以找出左焦點F1、 與它對應的節點N1、以及兩者間的距離f， 這個焦距值在理論上應該與（2）找出的值相等，不過在實務上很可能有稍許差異。

下面是一個例子，這個鏡頭有兩個凸透鏡，左邊凸透鏡的右焦點是圖中最右邊的方格，右邊凸透鏡的左焦點是圖中左緣的淺藍色方格。 從左方進入鏡頭的入射光（藍色）到達第一片透鏡會被折射到該透鏡的右焦點方向，但在到達它的右焦點前就遇到右邊的透鏡， 因此又被折射（用斜射光成像原理），最後與軸線在F2相交，這是鏡頭的右焦點。 把入射光與出射光延長（黑色點虛線）有一個交點，節面就是經過這個交點而且與軸線垂直的平面， 它和軸線的交點N2是與右焦點F2對應的節點， F2與N2之間的距離是鏡頭的焦距f。 反過來，用同樣的手續可以找出F1與N1。 請注意到這四者的順序是F1、N2、N1、 F2。

再看一個例子。 下圖的鏡頭有一個凸透鏡（左）與一個凹透鏡（右），凸透鏡右焦點是標了F2左邊的淺色方格， 凹透鏡右焦點是圖中最右邊的淺藍方格。 從左邊出發與軸線平行的入射光（藍色）到達凸透鏡時被折射向右邊的焦點，但在到達該焦點前遇到凹透鏡， 因而向外折射後與軸線在F2處相交，這是鏡頭右焦點； 經過入射光和出射光的延長線交點並且與軸垂直的平面是與F2對應的節面， 它和軸線的交點N2是與F2對應的節點。 追蹤從右邊進入鏡頭的光線（紅色）可以得到F1與N1， 這一次四個點的順序是F1、N1、N2、 F2。 從這個圖可以發現，鏡頭的焦距f比凸透鏡的焦距來得長； 換言之，在一個凸透鏡後方合適所在加一個凹透鏡可以加長凸透鏡的焦距，而且一個甚至兩個節點都可能在第一片透鏡前方， 這是望遠設計（telephoto）與增距鏡（也叫做加倍鏡）的基本原理。

把上面的鏡頭倒反過來，讓凹透鏡在前、凸透鏡在後（見下圖）， 如果適當選擇凹透鏡的位置與焦距，整個鏡頭的焦距要比原凸透鏡的來得短； 換言之，在凸透鏡前方加凹透鏡有縮短焦距的效果。 不但如此，一個甚至兩個節點都可能會出現在凸透鏡後方， 於是鏡頭的焦距f比焦平面到最後一片透鏡的距離 （這叫做鏡後距，back focal distance）來得短，這一類把望遠設計倒過來的設計叫做 倒裝望遠設計（retrofocus或reversed telephoto）， 是SLR/DSLR廣角鏡頭的最主要設計方式。

實例

了解節面、節點與焦點觀念之後不妨看幾個實際的例子，這些都是Nikon的老定焦鏡，因為變焦鏡的節點與焦點並不固定， 而近二十多年來廠商（包括Nikon在內）都不再出版這些資訊，所以此地的資料都是「古」書中得來。

下面是Nikkor-O 2.1cm f/4、Biogon類型的廣角鏡頭（1959年）， 圖中F與H是本文的F1與N1， 而F’與H’則是F2與N2； 另外，長度單位是mm。 首先注意到鏡後距（鏡頭最後一片透鏡到焦點F’的距離）是7.3mm，所以鏡頭離底片很近， 相機的反光鏡得要彈起並且鎖住才可以用這個鏡頭。 鏡頭的焦距（H’到F’的距離）是21mm，從下圖可以算出H’到最後透鏡的表面是13.7mm， 再從鏡頭總長47.5mm可以算出H到第一個透鏡表面的距離是9.5mm， 於是H與F的距離（左焦距）20.9mm = 11.4 + 9.5，幾乎是21mm。 請注意到這個鏡頭是個幾乎對稱的設計，兩個節點都在鏡頭內部。 有關Biogon的討論請看相機鏡頭： 對稱式廣角鏡頭（Hypergon、Topogon、Metrogon、Biogon與Hologon）一文。

下面是Nikkor-QD 15mm f/5.6（1973年），從H’與F’在鏡頭後方很遠、而且鏡後距是38.6mm兩點，我們就知道這是個倒裝望遠設計。 圖中從F到F’的距離是88.7mm，扣除H’與F’之間的距離（焦距）15.3mm與H到H’之間的距離58.1mm， 我們得到F與H之間的距離（左焦距）15.3mm。 請注意到H’與F’在鏡頭後方、F與H在鏡頭內部，倒裝望遠設計的廣角鏡頭差不多都如此。

下面是Nikkor-N 24mm f/2.8（1967年），另一個倒裝望遠設計的廣角鏡頭。 與Nikkor-QD 15mm f/5.6一樣，H’與F’在鏡頭後方、F與H在鏡頭內部：

接著看個標準鏡頭Nikkor-S 55mm f/1.2（1965年），這是個非對稱雙Gauss設計 （見相機鏡頭：Gauss、雙Gauss、Planar、Biotar等等一文的解釋）。 在這個設計中，H與H’位置互換而成為F、H’、H、F’的態勢，左焦距與右焦距有0.3mm的差異。 另外，左節點H移到鏡頭後方，右節點H’移到鏡頭內部，而且左焦點移到非常靠近鏡頭表面的位置。 事實上，從15mm到24mm、再到55mm，左焦點愈來愈向左移，雖然其它鏡頭未必全然如此。

底下是Nikkor-P 105mm f/2.5（1959年），這是Nikon早期的名鏡，所謂的Nikon 105王朝就是從這個鏡頭開始，不過它是Sonnar版 （見相機鏡頭：Ernostar與Sonnar一文的解釋）而不是後來更好的雙Gauss版。 請注意F與H的位置，兩者都移到鏡頭前方，而且H’就快到透鏡表面了。

把焦距再拉長一點是Nikon的另一個有名鏡頭Nikkor-P 180mm f/2.8（1970年），不過這不是1980年發表的ED版。 很明顯地，F、H與H’都移到鏡頭前方，雖然H’離第一片透鏡不遠，但已經有了望遠設計的味道。

下面是Nikkor-P 400mm f/5.6（1973年），這不是ED版（1975年）也不是ED-IF版（1978年）。 從圖中可以算出右節點H’在鏡頭第一片透鏡前方103.7mm，差不多是焦距的26%左右，所以望遠設計已經呼之欲出。

結論

這篇文章從直覺的焦點與焦距定義開始，先把薄透鏡近軸光學的基本部份簡單地做個介紹， 然後進入厚透鏡、再延伸到複透鏡，最後用幾個實例做結束。 用這麼長的篇幅說明焦點、節面、節點之間的關係有一個很重要的原因： 為日後其它基礎知識文章鋪路並且打下基礎。少了這些比較精準的觀念與知識，有些內容就很難說得清楚， 然而若為了簡單而全都用薄透鏡講解，固然結果淺顯易懂， 但得來的結論卻很容易被人往錯誤方向延伸而得到不正確的推論（譬如f值的定義）。 所以為了避免日後麻煩甚至可能誤導讀者，我們就走遠些、多講一點吧！

更新紀錄

  1. January 28, 2009上線.
  2. December 29, 2024搬家到此.