【冼鏡光初等幾何講堂】

May 24, 2023上線

2023年初在YouTube上看到幾個講日本寺廟幾何的影片， 有些用特例（譬如直角三角形三邊為3、4和5，求算什麼的，但是在一般情況下也能做得出來）、有些不夠嚴謹， 於是自已也做一做、試試推廣。讓我感到興趣的是，這些老師（大概是老師或教授吧）宣稱某些題目出自日本寺廟幾何； 我在1990年代初就買了一本叫做《San Gaku（算額）》的日本寺廟幾何問題集，但卻找不到若干被叫做日本寺廟幾何問題的問題。原因可能是我看漏了、播主記錯了、或其它原因。

看了若干集這些影片之後，總是覺得播主太照原題去解（譬如直角三角形3、4和5下的結果）、而沒有觸及比較深刻的層面；譬如，解答是否存在？是否唯一？推廣到一般情況下是否仍然有解？若有的話，解是否唯一？等等課題。

我是這樣想的：把這些以特例為主的題目往一般方向推廣一定很有意思，而且日本寺廟幾何問題中有不少極富巧思，拿出來和國內同學與老師分享是美事一件，所以我也想要拍一系列這樣的教學影片。然而，我的做法和一般教人解題的影片不同，我期望可以做點指引、也就是引導他人去思考、去綜合，從而能夠從比較高的位置看問題，希望我真的可以做到這一點。

順著這個方向，我會挑一些日本寺廟幾何問題出來討論、並旦把相關的放在一集中，以不超過初等微積分的層面探討這些問題。此外，我還想介紹一些初等幾何裡的漂亮定理（譬如，三角形各角的相鄰三等分角線交於一個正三角形 — Morley定理，三角形的九點圓和該三角形的內切圓以及三個外切圓相切 — Feuerbach定理，三角形中若有二分角線長度相同則必是等腰三角形，等等），有趣的初等幾何技巧（譬如倒形法、調和點列、交叉比、逆平行線等），再加上一些比較深的知識（三等分任意角不可能、五次和更高次的有理數係數多項式無法用加、減、乘、除和開方解、非歐幾何等等）。我會在有空時不定期錄製這些影片。

最後，我不會從YouTube收到一分一毫，此地全是非營利的學術義（或志）工行為。若您喜歡，比個讚、給個👍就好，並且和有興趣的同道分享。任何建設性、正面的建議和批評，請在YouTube上留言、或用email連繫。

以下是各講的影片和投影片。我也在籌劃一系列和程式設計、並行計算 （Concurrent Computing）有關的教學影片，有興趣的朋友不妨有空時來逛逛，看是否有新東西上線。

序號	題目和說明	影片連結	投影片	上線日期
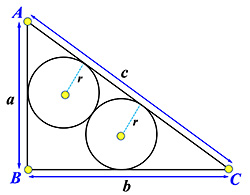
1	有兩個相互外切、相等半徑的圓，若它們都和一個直角三角形的斜邊相切， 而且每一個圓都和一直角邊相切。用直角三角形三邊長計算圓半徑。	第一講	第一講	April 9, 2023
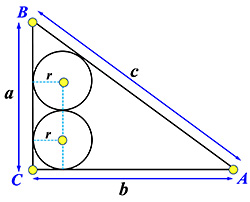
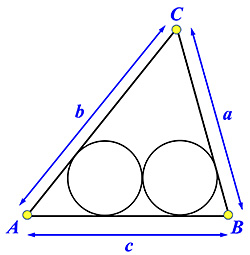
2	承上題。若兩個圓和一直角邊相切，而且一個圓和斜邊相切、另一圓和另一直角邊相切。 用直角三角形三邊長計算圓半徑。 若三角形不是直角形而是一般三角形時，結果又如何？	第二講	第二講	April 21, 2023
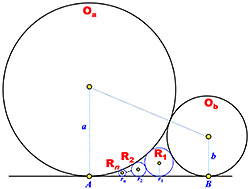
3	這一講會談到七道日本寺廟幾何問題，大致上分成兩類（第一節和第二節）。 在第一節，我們探討兩個外切的圓C1和C2，它們唯一地定義了第三個圓C3、它和C1與C2外切、 也和這兩個圓的公切線相切。試問C3的半徑是多少？進一步地說，C1和C3又定義出C4，C1和C4定出C5，等等。 如此一來，我們可以作出一串圓，請問Cn的半徑是多少？ 第二節則把上一節的問題反過來看。已知一個圓和它的一條弦，那麼和圓以及弦相切的衆小圓的半徑有何關係？ 答案是：這些小圓的半徑都可以很容易算出來，而且圓心在一條拋物線上。 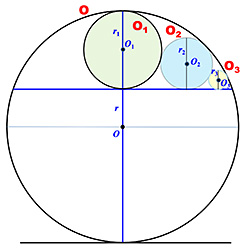最後，第三節把前兩節看似無關的問題串起來。假設一直線上有兩個定點， 於是兩個外切又和直線分別在定點上相切的圓會唯一地決定一個和該兩圓與直線相切的圓（第一節）。 因為這些被決定出來的小圓有無限個，我們問這些小圓之間有何關係？ 答案是，這些小圓和一個公切圓相切（第二節）、而且圓心在一條拋物線上。	第三講	第三講	August 12, 2023
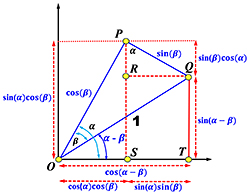
4	這是畢氏定理和畢氏等式三講中的第一講。Elisha Scott Loomis在他的1907年出版的名著『The Pythagorean Proposition』中說，不可能用三角學証明畢氏定理，因為三角學中的基本等式都源自畢氏定理，所以有畢氏定理才有三角學。 這個說法當然是錯的，這就是三講中第一講的主題。我們會證明角差和角和公式的正確性完全不會用到畢氏定理和畢氏公式，於是透過角差公式很容易就証明了畢氏等式。用角和公式証明畢氏等式稍許複雜些，我們先得到倍角公式不依賴畢氏定理和畢氏等式，再導出和差化積等式也不依賴畢氏定理和等式，然後再證明求sin(x)和cos(x)的導數也不依賴畢氏定理和等式，最後就從倍角公式導出畢氏等式了。更重要的是，知道這些知識之後、加上很簡單的微積分知識，畢氏等式就唾手可得。 接下來的兩講會專注在一個可能是畢氏定理的新証法和Jackson-Johnson的證明。為什麼Jackson-Johnson的證明值得討論呢？因為她們的證明用到了三角學、這在Loomis書中說是“不可能”的。我們會在第二講中討論一個可能是新的、証明畢氏的技巧，在第三講中說明Jackson-Johnson的證明。	第四講	第四講	December 18, 2023
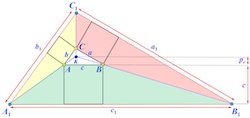
5	這是畢氏定理和畢氏等式的第二講。此地我們討論一個新的計算長度和面積的方法，透過這個新方法我們可以重新讓明Loomis書中的若干証明。不但如此，使用Lemoine點（或類似中心），我們還可以做出很可能是嶄新的若干證明。 下一講會討論Jackson和Johnson的證明。	第五講	第五講	December 27, 2023
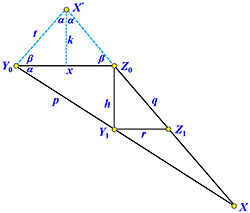
6	這是畢氏定理和畢氏等式的第三講。這一講中討論基於2023年由Jackson和Johnson發表（使用三角學）的純幾何證明；用Loomis的（錯誤）說法來看，Jackson-Johnson的三角學證明是“不可能”的，所以我們順Jackson-Johnson的思路給出一個純幾何的証明。接著，把這個純幾何証明稍做變化，就得到Jackson-Johnson的三角學証明。 這是本系列的最後一講，希望這連續有關畢氏定理三講對您有點幫助。	第六講	第六講	December 31, 2023