| Date: January 11 2024 | Title: MacMahon's sums-of-divisors and allied q-series |
| Speaker: Ken Ono | Abstract:
 |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Ken Ono slides |
|
Date: January 18 2024
11am US EDT | Title: Some unimodal sequences of Kronecker coefficients |
| Speaker: Alimzhan Amanov | Abstract: We conjecture unimodality for some sequences of generalized Kronecker coefficients and prove it for partitions with at most two columns. The proof is based on a hard Lefschetz property for corresponding highest weight spaces. We also study more general Lefschetz properties, show implications to a higher-dimensional analogue of the Alon–Tarsi conjecture on Latin squares and give related positivity results.
Joint work with Damir Yeliussizov. Please note the special time for this Seminar. |
| Affiliation: Kazakh-British Technical University |
| Video: | Video |
| Slides: | Alimzhan Amanov slides |
|
Date: January 25 2024 | Title: Combinatorial properties of triangular partitions |
| Speaker: Sergi Elizalde | Abstract: A triangular partition is a partition whose Ferrers diagram can be separated from its complement (as a subset of ℕ2) by a straight line. Having their origins in combinatorial number theory and computer vision, triangular partitions have been studied from a combinatorial perspective by Onn and Sturmfels, by Corteel et al., and by Bergeron and Mazin.
In this talk I will describe some new enumerative, geometric and algorithmic properties of such partitions. We give a new characterization of triangular partitions and the cells that can be added or removed (while preserving the triangular condition), and we study the poset of triangular partitions ordered by containment of their diagrams. Finally, using an encoding via balanced words, we give an efficient algorithm to generate all the triangular partitions of a given size, and a formula for the number of triangular partitions whose Young diagram fits inside a square.
This is joint work with Alejandro B. Galván. |
| Affiliation: Dartmouth |
| Video: | Video |
| Slides: | Sergi Elizalde slides |
|
Date: February 1 2024 | Title: Partition Hook Lengths |
| Speaker: Ajit Singh | Abstract: n 2010, G.-N. Han obtained the generating function for the number of size t hooks among integer partitions. In this talk, we discuss these generating functions for self-conjugate partitions, which are particularly elegant for even t. If nt(λ) is the number of size t hooks in a partition λ and SC denotes the set of self-conjugate partitions, then for even t we find that
∑λ ∈ SC xnt(λ) q|λ| = (-q;q2)∞ ˙ ((1-x2)q2t;q2t)∞t/2.
As a consequence, if at*(n) is the number of such hooks among the self-conjugate partitions of n, then for even t we obtain the simple formula
at*(n)=t∑j ≥ 1 q*(n-2tj),
where q*(m) is the number of partitions of m into distinct odd parts. As a corollary, we show that t | at*(n), which confirms a conjecture of Ballantine, Burson, Craig, Folsom and Wen.
This is joint work with Tewodros Amdeberhan, George E. Andrews, and Ken Ono. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Ajit Singh slides |
|
Date: February 8 2024 | Title: Applying Asymptotics Methods to Kang and Park's Generalization of the Alder-Andrews Theorem |
| Speaker: Leah Sturman | Abstract: We will discuss inequalities of integer partitions and the methods involved in proving such inequalities. In particular, the Alder-Andrews Theorem, a partition inequality generalizing Euler's partition identity, the first Rogers-Ramanujan identity, and a theorem of Schur to d-distinct partitions of n, was proved successively by Andrews in 1971, Yee in 2008, and Alfes, Jameson, and Lemke Oliver in 2010. While Andrews and Yee utilized q-series and combinatorial methods, Alfes et al. proved the finite number of remaining cases using asymptotics originating with Meinardus together with high-performance computing. In 2020, Kang and Park conjectured a "level 2" Alder-Andrews type partition inequality which relates to the second Rogers-Ramanujan identity. Duncan, Khunger, Swisher, and Tamura proved Kang and Park's conjecture for all but finitely many cases using a combinatorial shift identity. We generalize the methods of Alfes et al. to resolve nearly all of the remaining cases of Kang and Park's conjecture. |
| Affiliation: Bowdoin |
| Video: | Video |
| Slides: | Leah Sturman slides |
|
Date: February 15 2024 | Title: Palindrome Partitions and the Calkin-Wilf Tree |
| Speaker: Karlee Westrem | Abstract: There is a well-known bijection between finite binary sequences and integer partitions. Sequences of length r correspond to partitions of perimeter r+1. Motivated by work on rational numbers in the Calkin-Wilf tree, we classify partitions whose corresponding binary sequence is a palindrome. We give a generating function that counts these partitions, and describe how to efficiently generate all of them. Atypically for partition generating functions, we find an unusual significance to prime degrees. Specifically, we prove there are nontrivial palindrome partitions of n except when n=3 or n+1 is prime. We find an interesting new "branching diagram" for partitions, similar to Young's lattice, with an action of the Klein four group corresponding to natural operations on the binary sequences. |
| Affiliation: Michigan Technological University |
| Video: | Video |
| Slides: | Karlee Westrem slides |
|
Date: February 22 2024 | Title: Properties of sequentially congruent partitions |
| Speaker: Madeline Dawsey | Abstract: A sequentially congruent partition, defined by Schneider and Schneider in 2019, is a partition in which each part is congruent to the next part modulo its position in the partition. We introduce a new partition notation specific to sequentially congruent partitions which simplifies known partition bijections, illuminates their corresponding Young diagram transformations, and leads to generalizations of sequentially congruent partitions and related bijections. This is joint work with undergraduate students Ezekiel Cochran, Emma Harrell, and Samuel Saunders from the 2022 REU at the University of Texas at Tyler. |
| Affiliation: UT Tyler |
| Video: | Video |
| Slides: | Madeline Dawsey slides |
|
Date: February 29 2024 | Title: Analytic aspects of partitions with parts separated by parity |
| Speaker: Will Craig | Abstract: The study of partitions with parts separated by parity was initiated by Andrews in connection with Ramanujan's mock theta functions, and he produced many different variations of this theme. In this talk, we discuss analytic aspects of the generating functions originally produced by Andrews, including their relationship to modular forms and asymptotic formulas for their coefficients. Notably, one of our asymptotic formulas requires analyzing the error to modularity of a mock Maass theta function. |
| Affiliation: Universität zu Köln |
| Video: | Video |
| Slides: | Will Craig slides |
|
Date: March 7 2024 | Title: Identically vanishing coefficients in the series expansion of lacunary eta-quotients |
| Speaker: James McLaughlin | Abstract:
 |
| Affiliation: West Chester University |
| Video: | Video |
| Slides: | James McLaughlin slides |
|
Date: March 14 2024 | Title: Signed partition numbers |
| Speaker: Taylor Daniels | Abstract:
 |
| Affiliation: Purdue University |
| Video: | Video |
| Slides: | Taylor Daniels slides |
|
Date: March 21 2024 | Title: Frobenius partitions and automorphisms |
| Speaker: Nicolas Smoot | Abstract: We show that the Andrews-Sellers (AS) congruence family is part of a pair of closely related families for related Frobenius partition functions. We prove the second family via construction of a certain automorphism on a ℤ[t]-module of modular functions for Γ0(20) which permutes the module generators while fixing the modular functions for Γ0(5). To our knowledge, this is an entirely new method of proving p-adic convergence of modular function sequences. We also give some important insights into the behavior of these congruence families with respect to the Atkin-Lehner involution which proved very important in Paule and Radu's original proof of the AS congruences. This is joint work with James A. Sellers. |
| Affiliation: Universität Wien |
| Video: | Video |
| Slides: | Nicolas Smoot slides |
|
Date: March 28 2024 | Title: Double and triple perfect partitions |
| Speaker: Augustine Munagi | Abstract: A partition of a positive integer n is called perfect if it contains exactly one partition of each positive integer less than n. A partition is double-perfect if it contains two partitions of each integer between 2 and n-2. Both perfect and double-perfect partitions are known to be enumerated by ordered factorization functions. In this talk we give new proofs of the results on double-perfect partitions based on insertions of special summands into perfect partitions and propose a definition of p-perfect partitions for any integer p>0. Then we apply the new approach to the study of partitions of n containing three partitions of every integer in the interval [m, n-m] for certain values of m ≥ 3. |
| Affiliation: Univ. of the Witwatersrand |
| Video: | Video |
| Slides: | Augustine Munagi slides |
|
| Date: April 11 2024 | Title: Fixed points in first-column hook lengths |
| Speaker: William Keith | Abstract: Recently, Blecher and Knopfmacher applied the notion of fixed points to integer partitions. This has already been generalized and refined in various ways, such as h-fixed points by Hopkins and Sellers. Here we consider the sequence of first column hook lengths in the Young diagram of a partition and corresponding fixed hooks. We enumerate these, using both generating function and combinatorial proofs, and find that they match occurrences of part sizes equal to their multiplicity. We establish connections to work of Andrews and Merca on truncations of the pentagonal number theorem and classes of partitions partially characterized by certain minimal excluded parts (mex). This is joint work with Philip Cuthbertson, David Hemmer, and Brian Hopkins. |
| Affiliation: Michigan Tech |
| Video: | Video |
| Slides: | William Keith slides |
|
| Date: April 18 2024 | Title: On partitions with bounded largest part and fixed integral GBG-rank modulo primes |
| Speaker: Aritram Dhar | Abstract: In 2009, Berkovich and Garvan introduced a new partition statistic called the GBG-rank modulo t which is a generalization of the well-known BG-rank. In this talk, we explain the use of Littlewood decomposition of partitions to study partitions with bounded largest part and fixed integral value of GBG-rank modulo primes. As a consequence, we obtain new elegant generating function formulas for unrestricted partitions, self-conjugate partitions, and partitions whose parts repeat finite number of times. This is joint work with Alexander Berkovich. |
| Affiliation: UFL |
| Video: | Video |
| Slides: | Aritram Dhar slides |
|
| Date: April 25 2024 | Title: A new Series for Rogers-Ramanujan-Gordon at k=3 |
| Speaker: Yalçın Can Kılıç | Abstract: The Rogers-Ramanujan identities have a central role in integer partitions. They were extended combinatorially by Gordon in 1961. Andrews found an analytic representation for the Rogers-Ramanujan-Gordon identities in 1974. In this talk, a new evidently positive generating function for the difference condition side of Rogers-Ramanujan-Gordon partitions when k=3 is given. Also, it is combinatorially interpreted using the base partition-moves framework. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Yalçın Can Kılıç slides |
|
| Date: September 7 2023 | Title: Partition Fixed Points: Connections, Generalizations, and Refinements |
| Speaker: Brian Hopkins | Abstract: Last year, Blecher and Knopfmacher introduced the idea of a fixed point to integer partitions, such as those with second part 2. For partitions presented in nonincreasing order, they made a conjecture about the number with or without a fixed point. We confirmed their conjecture by connecting fixed points to a growing network of related partition statistics: the Frobenius symbol, Dyson's crank, and the mex (minimal excludant). For generalizations, shifting the fixed point criterion to, e.g., second part 4, gives a family of results connected to the crank and related to a generalized mex defined by the speaker, Sellers, and Stanton. For refinements, the integer triangle determined by counting partitions with a particular fixed point has many interesting patterns including analogues of Pascal's lemma and identities for both diagonal and antidiagonal sums. Much of this is joint work with James Sellers. |
| Affiliation: St. Peter's |
| Video: | Video |
| Slides: | Brian Hopkins slides |
|
| Date: September 14 2023 | Title: A Decomposition of Cylindric Partitions and Cylindric Partitions into Distinct Parts |
| Speaker: Kağan Kurşungöz | Abstract: We show that cylindric partitions are in one-to-one correspondence with a pair which has an ordinary partition and a colored partition into distinct parts. Then, we show the general form of the generating function for cylindric partitions into distinct parts and give some examples. We prove part of a conjecture by Corteel, Dousse, and Uncu. The approaches and proofs are elementary and combinatorial.
This is joint work with Halime Ömrüuzun Seyrek.
The arxiv preprint is at https://arxiv.org/abs/2308.14514 , some updates due to updates in Warnaar's work will be incorporated in the near future. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Kağan Kurşungöz slides
Kağan Kurşungöz slides, annotated |
|
| Date: September 21 2023 | Title: Cultivating Maple and Sage in Ramanujan's Garden |
| Speaker: Frank Garvan | Abstract: This talk is on experimental math and how we can use Maple and Sage to gain insight into various rank and crank type functions. Includes some joint work with Rishabh Sarma. |
| Affiliation: Univ. of Florida |
| Video: | Video |
| Slides: | Frank Garvan slides (pdf)
Frank Garvan slides, raw Maple workbook |
|
| Date: September 28 2023 | Title: Infinite families of congruences modulo powers of 2 for partitions into odd parts with designated summands |
| Speaker: James Sellers | Abstract: In 2002, Andrews, Lewis, and Lovejoy introduced the combinatorial objects which they called partitions with designated summands. These are built by taking unrestricted integer partitions and designating exactly one of each occurrence of a part. In that same work, Andrews, Lewis, and Lovejoy also studied such partitions wherein all parts must be odd. Recently, Herden, Sepanski, Stanfill, Hammon, Henningsen, Ickes, and Ruiz proved a number of Ramanujan-like congruences for the function PDO(n) which counts the number of partitions of weight n with designated summands wherein all parts must be odd. In the first part of this talk, we will use truly elementary techniques to prove some of the results conjectured by Herden, et. al. by proving the following two infinite families of congruences satisfied by PDO(n):
For all k ≥ 0 and n ≥ 0,
PDO(2k(4n+3)) ≡ 0 (mod 4) and
PDO(2k(8n+7)) ≡ 0 (mod 8).
We will then transition to a discussion of the following unexpected infinite family of internal congruences:
For all k ≥ 0 and all n ≥ 0,
PDO(22k+3n) ≡ PDO(22k+1n) (mod 22k+3).
This family of results is proven via generating function dissections, various modular relations and recurrences involving a Hauptmodul on the classical modular curve X0(6), and an induction argument which provides the final step in proving the necessary divisibilities. This latter result is joint work with Shane Chern, Dalhousie University. |
| Affiliation: UMN-Duluth |
| Video: | Video |
| Slides: | James Sellers slides |
|
| Date: October 5 2023 | Title: New Infinite Hierarchies Of Polynomial Identities Related To The Capparelli Partition Theorems |
| Speaker: Ali Uncu | Abstract: We will talk about the polynomial refinements of Capparelli's identities and the beautiful infinite families of identities they give rise to.
This is joint work with Alexander Berkovich. |
Affiliation: Austrian Acad. of Sciences
Univ. of Bath |
| Video: | Video |
| Slides: | Ali Uncu slides |
|
| Date: October 12 2023 | Title: Methods in asymptotic statistics for partitions |
| Speaker: Walter Bridges | Abstract: Choose a partition of a large number uniformly at random. How big do we expect the largest part to be? How many 1's are there? What does the Young diagram look like? For that matter, how can we generate large partitions efficiently, to collect data and make conjectures?
In the first part of this talk, we will give an overview of the so-called Boltzmann model for partitions, a technique developed in the 90s by Fristedt, Pittel, Vershik and others for answering the above questions. Time permitting, we will sketch proofs of the distribution of small parts, the largest part, limit shapes for Young diagrams, and even the asymptotic formula for p(n), the number of partitions of n.
In the second part of this talk, we discuss the speaker's adaptation of these techniques to unimodal sequences and partitions with gap conditions. This is joint work with Kathrin Bringmann. |
| Affiliation: Universität zu Köln |
| Video: | Video |
| Slides: | Walter Bridges slides |
|
|
Date: October 19 2023
8pm US EDT | Title: Bressoud's Conjecture on the Rogers-Ramanujan Identities |
| Speaker: Kathy K. Q. Ji | Abstract: In 1980, Bressoud put forward a conjecture for a more general partition identity that implies many classical results in the theory of partitions. The general case for j=1 was recently resolved by Kim. In this talk, we present an answer to Bressoud's conjecture for the case j=0, resulting in a complete solution to the conjecture. It is somewhat unexpected that overpartitions play a crucial role in this regards.
For a fuller abstract, see this pdf.
Please note the special time for this Seminar.
|
| Affiliation: Tianjin University |
| Video: | Video |
| Slides: | Kathy Q. Ji slides |
|
| Date: October 26 2023 | Title: Neighborly partitions, hypergraphs and Gordon's identities |
| Speaker: Pooneh Afsharijoo | Abstract: The family of Gordon's identities is an important family of partition identities which generalizes the famous Rogers-Ramanujan identities. We prove a family of partition identities which is "dual" in a some sense (that we will explain) to Gordon's identities. These new identities make intervene a new type of partitions (the (r, i)-Neighborly partitions) and the hypergraphs (generalization of graphs) associated with them. This is a joint work with H. Mourtada; it generalizes a recent work by Z. Mohsen and H. Mourtada in which they give new partition identities which are dual to those of Rogers-Ramanujan. |
| Affiliation: Univ. Complutense Madrid |
| Video: | Video |
| Slides: | Pooneh Afsharijoo slides |
|
|
Date: November 2 2023
10am US EDT | Title: Asymptotic and exact formulas in the theory of partitions |
| Speaker: Kathrin Bringmann | Abstract: In this talk I will explain asymptotics of various partition statistic and how modularity helps to show such behaviors. Besides the classical modular forms I will also speak about mock theta functions and false theta functions.
Please note the special time for this Seminar.
|
| Affiliation: Universität zu Köln |
| Video: | Video |
| Slides: | Kathrin Bringmann slides |
|
| Date: November 9 2023 | Title: N-colored generalized Frobenius partitions: Generalized Kolitsch identities |
| Speaker: Zafer Selcuk Aygin | Abstract: We establish an asymptotical formula for the number of N-colored generalized Frobenius partitions of n in terms of the partition function. These results are from a joint work with Professor Khoa Dang Nguyen of the University of Calgary.
For a fuller abstract, see this pdf.
|
| Affiliation: Northwestern Polytechnic |
| Video: | Video |
| Slides: | Zafer Selcuk Aygin slides |
|
| Date: November 30 2023 | Title: d-Fold Partition Diamonds: Generating Functions and Partition Analysis |
| Speaker: Dalen Dockery | Abstract: This is the first in a sequence of two talks concerning d-fold partition diamonds. These combinatorial objects generalize both classical partitions and the plane diamond partitions introduced by Andrews, Paule, and Riese in 2001, as well as their Schmidt type counterparts (obtained by only using parts of certain indices). We use MacMahon's theory of partition analysis to find generating functions for this family of partitions. Along the way, we prove a result that extends several of MacMahon's elimination formulae to an arbitrary number of terms. To conclude this talk, we simplify the generating functions in the case of Schmidt type partitions by appealing to a result of Euler on Eulerian polynomials.
This is joint work with Marie Jameson, James A. Sellers, and Samuel Wilson.
Two-part series with James Sellers. |
| Affiliation: UT-Knoxville |
| Video: | Video |
| Slides: | Dalen Dockery slides |
|
| Date: December 7 2023 | Title: Arithmetic Properties of d-fold Partition Diamonds |
| Speaker: James Sellers | Abstract: This is the second in a sequence of two talks concerning d-fold partition diamonds and serves as a continuation of Dalen Dockery's talk from the previous week. We will begin with a brief reminder of the topic, including the generating functions involved. Once that review is complete, we will use the generating functions in question to provide elementary proofs of infinitely many Ramanujan-like congruences satisfied by d-fold partition diamonds.
This is joint work with Dalen Dockery, Marie Jameson, and Samuel Wilson.
Two-part series with Dalen dockery. |
| Affiliation: UMN-Duluth |
| Video: | Video |
| Slides: | James Sellers slides |
|
| Date: January 19 2023 | Title: Self-conjugate 6-cores and quadratic forms |
| Speaker: Marie Jameson | Abstract: We will analyze the behavior of the self-conjugate 6-core partition numbers sc6(n) by utilizing the theory of quadratic and modular forms. In particular, we explore when sc6(n) > 0. Positivity of sct(n) has been studied in the past, and Hanusa and Nath conjectured that sc6(n) > 0 except when n ∈ {2, 12, 13, 73}. Assuming the Generalized Riemann Hypothesis, we are able to settle Hanusa and Nath's conjecture. |
| Affiliation: UT-Knoxville |
| Video: | Video |
| Slides: | Marie Jameson slides |
|
| Date: January 26 2023 | Title: Forgotten conjectures of Andrews for Nahm-type sums |
| Speaker: Joshua Males | Abstract: In his famous '86 paper, Andrews made several conjectures on the function σ(q) of Ramanujan, including that it has coefficients (which count certain partition-theoretic objects) whose sup grows in absolute value, and that it has infinitely many Fourier coefficients that vanish. These conjectures were famously proved by Andrews-Dyson-Hickerson in their '88 Invent. paper, and the function σ has been related to the arithmetic of ℤ[√6] by Cohen (and extensions by Zwegers), and is an important first example of quantum modular forms introduced by Zagier.
A closer inspection of Andrews' '86 paper reveals several more functions that have been a little left in the shadow of their sibling σ, but which also exhibit extraordinary behaviour. In an ongoing project with Folsom, Rolen, and Storzer, we study the function v1(q) which is given by a Nahm-type sum and whose coefficients count certain differences of partition-theoretic objects. We give explanations of four conjectures made by Andrews on v1, which require a blend of novel and well-known techniques, and reveal that v1 should be intimately linked to the arithmetic of the imaginary quadratic field ℤ[√(-3)]. |
| Affiliation: Univ. of Manitoba |
| Video: | Video |
| Slides: | Joshua Males slides |
|
| Date: February 2 2023 | Title: Ramanujan-Kolberg identities, regular partitions, and multipartitions |
| Speaker: William J. Keith | Abstract: Ramanujan-Kolberg identities relate subprogressions of the partition numbers and linear combinations of eta-quotients, so named after Ramanujan's "most beautiful identity" ∑m ≥ 0 p(5m+4) qn = 5 ∏n ≥ 1 (1-q5n)5 / (1-qn)6. Descending from equality to congruence mod 2, recent work of the speaker and Fabrizio Zanello has produced a large number of these with implications for the study of the parity of the partition function, and Shi-Chao Chen has shown that these are part of an infinite family where the eta-quotients required have a very small basis. Analyses of particular cases from that family yield many pleasing patterns: older work of the speaker and Zanello gave congruences for the m-regular partitions for m odd, and this talk will be on more recent joint work which exhibits the very different behavior for m even which gives connections to multipartitions. All of these results in turn illuminate different aspects of the longstanding partition parity problem and hopefully provide some useful insight therein.
This is joint work with Fabrizio Zanello. |
| Affiliation: Michigan Technological University |
| Video: | Video |
| Slides: | William Keith slides |
|
| Date: February 9 2023 | Title: Some Legendre theorems for a class of partitions with early conditions |
| Speaker: Darlison Nyirenda | Abstract: In this talk, we consider a subclass of partitions with early conditions, introduced by George E. Andrews. We present Legendre theorems associated with these partitions. The theorems provide combinatorial interpretation of some Rogers-Ramanujan identities due to Lucy J. Slater. |
| Affiliation: Univ. of the Witwatersrand |
| Video: | Video |
| Slides: | Darlison Nyirenda slides |
|
| Date: February 23 2023 | Title: A Unified Approach to Unimodality of Gaussian Polynomials |
| Speaker: Ali K. Uncu | Abstract: In 2013, Pak and Panova proved the strict unimodality property of Gaussian Polynomials (a.k.a. q-binomial coefficients) 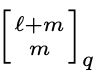 , as polynomials in q. They showed it to be true for all ℓ, m ≥ 8 and a few other cases. We propose a different approach to this problem based on computer algebra, where we establish a closed form for the coefficients of these polynomials and then use cylindrical algebraic decomposition to identify exactly the range of coefficients where strict unimodality holds. This strategy allows us to tackle generalizations of the problem, e.g., to show unimodality with larger gaps or unimodality of related sequences. In particular, we present proofs of two additional cases of a conjecture by Stanley and Zanello. , as polynomials in q. They showed it to be true for all ℓ, m ≥ 8 and a few other cases. We propose a different approach to this problem based on computer algebra, where we establish a closed form for the coefficients of these polynomials and then use cylindrical algebraic decomposition to identify exactly the range of coefficients where strict unimodality holds. This strategy allows us to tackle generalizations of the problem, e.g., to show unimodality with larger gaps or unimodality of related sequences. In particular, we present proofs of two additional cases of a conjecture by Stanley and Zanello.
This is a joint work with Christoph Koutschan and Elaine Wong. For more data, see https://wongey.github.io/unimodality/. |
| Affiliation: RICAM-AAS |
| Video: | Video |
| Slides: | Ali Uncu slides |
|
| Date: March 2 2023 | Title: On some new "multi-sum = product" identities |
| Speaker: Shashank Kanade | Abstract: Recently, in a joint work with Baker, Sadowski and Russell, motivated by vertex-algebraic considerations, certain new "multi-sum = product" identities emerged. Significantly, we found and proved a quadruple-sum representation for Nandi's identities. Additionally, we found and proved a set of new identities where the mod-10 products are the same as in level 4 principal characters of the affine Lie algebra D4(3). (Recall that some of the earlier mod-9 conjectures of the speaker jointly with Russell were about level 3 principal characters of the affine Lie algebra D4(3).) I will explain these developments and give a sketch of the computational technique behind the proofs. |
| Affiliation: Univ. of Denver |
| Video: | Video |
| Slides: | Shashank Kanade slides |
|
| Date: March 16 2023 | Title: Localization Applied to a Genus 1 Congruence Family. |
| Speaker: Nicolas Smoot | Abstract: Over the last century, a large variety of infinite congruence families have been discovered and studied for different integer partition functions. These families exhibit a great variety with respect to the difficulty of their proof: some have been understood for decades, while others are still resistant to proof today. Major complicating factors arise from the topology of the associated modular curve: classical techniques are sufficient when the associated curve has cusp count 2 and genus 0; as either number grows, the difficulty of the congruence family grows. In recent years we have developed a systematic method for handling families in which the genus is 0 but the cusp count is greater than 2. We will report on the successful extension of localization to a congruence family in the case of genus 1, for the 2-elongated plane partition diamond counting function d2(n) by powers of 7. We compare our method with other techniques for proving genus 1 congruence families, and discuss the implications regarding the overall classification of the subject. We finally conjecture a second congruence family for d3(n) by powers of 7 which should be amenable to similar techniques.
This is joint work with Koustav Banerjee. |
| Affiliation: RISC-Linz |
| Video: | Video |
| Slides: | Nicolas Smoot slides |
|
| Date: March 23 2023 | Title: Counting matrix points on curves and surfaces with partitions |
| Speaker: Hasan Saad | Abstract: Partitions are ubiquitous in mathematics appearing in combinatorics, number theory, and representation theory. Here we discuss how partitions make it possible to count "matrix" points on curves and surfaces over finite fields. Using partition generating function formulas of Euler, Feit and Fine counted the number of n × n commuting matrices over finite fields. Building on this classical result, it is natural to count the number of "matrix" points over finite fields on curves and surfaces. In this talk we show how to employ partitions and Gaussian hypergeometric functions to count such n × n matrix points on elliptic curves and certain K3 surfaces. We then use these results to determine the Sato-Tate distribution of these points counts. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Hasan Saad slides |
|
| Date: March 30 2023 | Title: General coefficient-vanishing results associated with theta series |
| Speaker: Shane Chern | Abstract: There are a number of sporadic coefficient-vanishing results associated with theta series, which suggest certain underlying patterns. By expanding theta powers as a linear combination of products of theta functions, we present two strategies that will provide a unified treatment. Our approaches rely on studying the behavior of a product of two theta series under the action of the huffing operator. For this purpose, some explicit criteria are given. We may use the presented methods to not only verify experimentally discovered coefficient-vanishing results, but also to produce a series of general phenomena. |
| Affiliation: Dalhousie Univ. |
| Video: | Video |
| Slides: | Shane Chern slides |
|
| Date: April 13 2023 | Title: Combinatorial proofs and refinements of three partition theorems of Andrews |
| Speaker: Shishuo Fu | Abstract: In his recent work, Andrews revisited two-color partitions with certain restrictions on the differences between consecutive parts, and he established three theorems linking these two-color partitions with more familiar kinds of partitions, such as strict partitions and basis partitions. In this talk, we present bijective proofs as well as refinements of those three theorems of Andrews. Our refinements take into account the numbers of parts in each of the two colors.
NOTE SPECIAL TIME: This talk is scheduled for 7pm US EDT, 5 hours later than usual, to accommodate a speaker from China. |
| Affiliation: Chongqing Univ. |
| Video: | Video |
| Slides: | Shishuo Fu slides |
|
| Date: Sep 1 2022 | Title: Biases in parts among k-regular and k-indivisible partitions |
| Speaker: Faye Jackson and Misheel Otgonbayar | Abstract: For integers k, t ≥ 2 and 1 ≤ r ≤ t, let Dk(r, t, n) and Dk×(r, t, n) be the number of parts that are congruent to r mod t among partitions of n that are k-regular (no parts repeating k or more times) and k-indivisible (no parts divisible by k) respectively. Using the circle method, we find the asymptotic for each quantity as n tends to infinity. From this asymptotic, we find that in both k-regular and k-indivisible cases, the parts are weakly equidistributed among equivalence classes mod t. However, inspection of the lower order terms implies a bias towards the lower congruence classes for k-regular partitions; that is, for 1 ≤ r < s ≤ t, we have Dk(r, t, n) ≥ Dk(s, t, n) for large n. We make this inequality explicit. In the k-indivisible case however, the bias is much more chaotic due to the interaction of the multiplicative structures mod k and t. Most notably, while the k-regular case matches with a simple combinatorial heuristic, there appears to be no such heuristic for the k-indivisible partitions. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Jackson and Otgonbayar slides |
|
| Date: Sep 15 2022 | Title: Elementary Proofs of Infinite Families of Congruences for Merca's Cubic Partitions |
| Speaker: James Sellers | Abstract: In the September 2022 issue of the Ramanujan Journal, Mircea Merca published a paper whose focus was on the function A(n) which is defined to be the difference between the number of cubic partitions of n into an even number of parts and the number of cubic partitions of n into an odd number of parts. (Recall that a cubic partition is a partition wherein the even parts are allowed to appear in two different colors.)
Recently, using modular forms and Smoot's Mathematica implementation of Radu's algorithm for proving partition congruences, Merca proved the following two congruences: For all n ≥ 0,
A(9n+5) ≡ 0 mod 3,
A(27n+26) ≡ 0 mod 3.
In this talk, we will provide elementary proofs of these two congruences via classical generating function manipulations. We then prove two infinite families of non--nested Ramanujan--like congruences modulo 3 satisfied by A(n) wherein Merca's original two congruences serve as the initial members of each family.
This is joint work with Robson da Silva, Universidade Federal de Sao Paulo, Brazil. |
| Affiliation: UMN-Duluth |
| Video: | Video |
| Slides: | James Sellers slides |
|
| Date: Sep 22 2022 | Title: Bijective approaches for Schmidt type theorems |
| Speaker: Hunter Waldron | Abstract: We study two bijections to find new Schmidt type theorems, which concern the equinumerosity of partitions with parts counted at only given indices, and other more well studied families of partitions. First, we show that Mork's bijection, originally given as a proof of Schmidt's theorem, is identical to an older bijection of Bessenrodt when applied to a 2-modular diagram, which implies a Schmidt type refinement of Euler's theorem. We then develop an idea from a recent paper of Andrews and Keith to construct a bijection between partitions counted at the indices r, t+r, 2t+r, ... and t-colored partitions. |
| Affiliation: MTU |
| Video: | Video |
| Slides: | Hunter Waldron slides |
|
| Date: Sep 29 2022 | Title: Hook Length and Symplectic Content in Partitions |
| Speaker: Cristina Ballantine | Abstract: The irreducible polynomial representations of the general linear group are indexed by partitions. The dimension of a representation is given by a formula involving the hook lengths and the contents of cells in the Young diagram of the indexing partition. There are also analogous formulas for irreducible polynomial representations of symplectic and orthogonal groups. I will discuss the combinatorial nature of identities involving hooks and the symplectic (and orthogonal) contents. These have been conjectured by T. Amdeberhan and are inspired by the Nekrasov-Okounkov hook-length formula. Time permitting, I will also introduce some auxiliary results. The representation theory is mentioned only as motivation and I will not discuss it further in the talk. (Joint work with Tewodros Amdeberhan and George Andrews.) |
| Affiliation: Holy Cross |
| Video: | Video is available upon request; please email host or speaker. |
| Slides: | Cristina Ballantine slides |
|
| Date: Oct 6 2022 | Title: Partitions, Kernels, and Localization |
| Speaker: Nicolas Smoot | Abstract: Since Ramanujan's groundbreaking work, there has been a large variety of infinite congruence families for partition functions modulo prime powers. These families vary enormously with respect to the difficulty of proving them. We will discuss the application of the localization method to proving congruence families by walking through the proof of one recently discovered congruence family for the counting function for 5-elongated plane partitions. In particular, we will discuss a critical aspect of such proofs, in which the associated generating functions of a given congruence family are members of the kernel of a certain linear mapping to a vector space over a finite field. We believe that this approach holds the key to properly classifying congruence families. |
| Affiliation: RISC-Linz |
| Video: | Video |
| Slides: | Nicolas Smoot slides |
|
| Date: Oct 13 2022 | Title: Combinatorial constructions of generating functions of cylindric partitions with small profiles into unrestricted or distinct parts |
| Speaker: Halime Ömrüuzun Seyrek | Abstract: Cylindric partitions into profiles c=(1,1) and c=(2,0) are considered. The generating functions into unrestricted cylindric partitions and cylindric partitions into distinct parts with these profiles are constructed. The constructions are combinatorial and they connect the cylindric partitions with ordinary partitions. The generating function of cylindric partitions with the said profiles turn out to be combinations of two infinite products. This is a joint work with Kağan Kurşungöz. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Halime Ömrüuzun Seyrek slides |
|
| Date: Nov 3 2022 | Title: Finding odd values of p(n) |
| Speaker: Catherine Cossaboom and Sharon Zhou | Abstract: One of the deepest open problems in the theory of partitions is the assertion that 50% of the values of p(n) are even (resp. odd). Very little is known in the direction of this conjecture. The best known lower bounds for the number of even (resp. odd) values relies on variants of Euler's classical recurrence for p(n), typically souped up with the theory of modular forms. In this talk, we will introduce a new framework that explicitly provides infinitely many such relations. These results follow from the phenomenon of Hecke nilpotency. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Cossaboom and Zhou slides |
|
| Date: Nov 10 2022 | Title: Basic hypergeometric summation theorems with symmetry in four variables |
| Speaker: Jonathan Bradley-Thrush | Abstract: The 6φ5 summation theorem of L.J. Rogers has a formulation, due to F.H. Jackson, which is symmetrical with respect to three of its parameters. I will re-examine the problem, first considered by Jackson, of extending Rogers's identity to one which possesses a fourfold symmetry. Analogous to Jackson's formulation of the 6φ5 summation theorem, there is a form of Bailey's 6ψ6 identity which is symmetrical in three parameters. Motivated by this, I will present a bilateral summation theorem with symmetry in four variables, giving an outline proof and briefly examining a few interesting special cases. The theory of WZ pairs will be employed to obtain further results; some partial fraction expansions will also be considered. I will conclude with the statements of a few open problems. |
| Affiliation: Univ. of Florida |
| Video: | Video |
| Slides: | Jonathan Bradley-Thrush slides |
|
| Date: Nov 17 2022 | Title: Composition-theoretic series in partition theory |
| Speaker: Robert Schneider and Drew Sills | Abstract: We use sums over integer compositions analogous to generating functions in partition theory, to express certain partition enumeration functions as sums over compositions into parts that are k-gonal numbers; our proofs employ Ramanujan's theta functions. We explore applications to lacunary q-series, and to a new class of composition-theoretic Dirichlet series. |
| Affiliation: MTU and GSU |
| Video: | Video |
| Slides: | Sills slides and Schneider slides |
|
| Date: Dec 1 2022 | Title: Modulo d extension of parity results in Rogers-Ramanujan-Gordon type overpartition identities |
| Speaker: Kağan Kurşungöz | Abstract: Sang, Shi and Yee, in 2020, found overpartition analogs of Andrews' results involving parity in Rogers-Ramanujan-Gordon identities. Their result partially answered an open question of Andrews'. The open question was to involve parity in overpartition identities. We extend Sang, Shi, and Yee's work to arbitrary moduli, and also provide a missing case in their identities. We also unify proofs of Rogers-Ramanujan-Gordon identities for overpartitions due to Lovejoy and Chen et. al.; Sang, Shi, and Yee's results; and ours. Although verification type proofs are given for brevity, a construction of series as solutions of functional equations between partition generating functions is sketched. This is joint work with Mohammad Zadehdabbagh. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Kurşungöz slides and slides with written notes |
|
| Date: Dec 8 2022 | Title: Recent problems in partitions and other combinatorial functions |
| Speaker: Larry Rolen | Abstract: In this talk, I will discuss recent work, joint with a number of collaborators, on analytic and combinatorial properties of the partition and related functions. This includes work on recent conjectures of Stanton, which aim to give a deeper understanding into the "rank" and "crank" functions which "explain" the famous partition congruences of Ramanujan. I will describe progress in producing such functions for other combinatorial functions using the theory of modular and Jacobi forms and recent connections with Lie-theoretic objects due to Gritsenko-Skoruppa-Zagier. I will also discuss how analytic questions about partitions can be used to study Stanton's conjectures, as well as recent conjectures on partition inequalities due to Chern-Fu-Tang and Heim-Neuhauser, which are related to the Nekrasov-Okounkov formula. |
| Affiliation: Vanderbilt University |
| Video: | Video |
| Slides: | Larry Rolen slides |
|
| Date: Jan 20 2022 | Title: Statistical distributions on integer partitions |
| Speaker: Ken Ono | Abstract: In this talk we examine three types of distributions on integer partitions.
(1) Generalizing a classical theorem of Erdos and Lehner, we determine the distribution of parts in partitions that are multiples of a fixed integer A. For example, the case of A=2 is the case of even parts in partitions of a large integer n. These limiting distributions are of Gumbel type, which are used to predict earthquakes! These results have implications in the algebraic geometry of n point Hilbert schemes.
(2) For a fixed positive integer t, we determine the distribution of the number of hook lengths of size t among the partitions of n. As n tends to infinity, the distributions are asymptotically normal.
(3) For a fixed integer t > 3, we determine the distribution of the number of hook lengths that are multiples of t among the partitions of n. As n tends to infinity, the distributions are asymptotically shifted Gamma distributions.
This is joint work with Michael Griffin, Larry Rolen, and Wei-Lun Tsai. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Ken Ono slides |
|
| Date: Jan 27 2022 | Title: A Conjecture on Seaweed Algebras and Partitions |
| Speaker: William Craig | Abstract: In 2018 Coll, Mayers and Mayers initiated the study of the index statistic of seaweed algebras from a partition-theoretic point of view. Within their framework, they conjecture that the difference between the number of partitions into odd parts having odd index and those with even index has the peculiar generating function (q, -q3; q4)∞-1. We prove this conjecture using a variation of the circle method and Euler-Maclaurin summation. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | William Craig slides |
|
| Date: Feb 10 2022 | Title: Partition identities with eventually periodic residue conditions |
| Speaker: Kağan Kurşungöz | Abstract: The majority of integer partition identities relate gap conditions to residue conditions. Gap conditions control how many times a part can appear in the partitions, and residue conditions stipulate which parts can appear without a bound on the number of repetitions. Kanade and Russell in 2015 developed a computerized method to discover partition identities, and made a fundamental change in our paradigm. In a PURE project in the summer of 2021, students implemented a variant of Kanade and Russell's IdentityFinder to discover partition identities with a novel theme, namely "eventually periodic residue conditions". Most of these identities can be proven by elementary means, some of them require transformations to be recognized as corollaries of known results. There is one new construction of an evidently positive generating function due to a lucky mistake. This is the preliminary report on joint work with Salih Numan Büyükbaş, Vahit Alp Hıdıroğlu, and Ömer Surhay Kocakaya, our graduate students. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Kağan Kurşungöz slides |
|
| Date: Feb 17 2022 | Title: Construction of Evidently Positive Series and An Alternative Construction for a Family of Partition Generating Functions due to Kanade and Russell |
| Speaker: Halime Ömrüuzun Seyrek | Abstract: We give an alternative construction for a family of partition generating functions due to Kanade and Russell. In our alternative construction, we use ordinary partitions instead of jagged partitions. We also present new generating functions which are evidently positive series. To obtain those generating functions, we first construct an evidently positive series for a key infinite product. In that construction, a series of combinatorial moves is used to decompose an arbitrary partition into a base partition together with some auxiliary partitions that bijectively record the moves.
This is a joint work with Prof. Kağan Kurşungöz. |
| Affiliation: Sabancı Üniversitesi |
| Video: | Video |
| Slides: | Halime Ömrüuzun Seyrek slides |
|
| Date: Mar 3 2022 | Title: Generalizations and refinements of Schmidt's Theorem |
| Speaker: William J. Keith | Abstract: Recently, George Andrews spoke in this Seminar on the theorem of Schmidt that the statistic summing only odd parts of partitions into distinct parts has the same distribution as the ordinary weight on all partitions. We show that this theorem can be generalized to partitions into parts appearing fewer than m times, and counting parts in various places modulo m, yielding tidy generating functions for colored partitions. This count can then be further refined by the number of parts of each color appearing. Additional questions present themselves for further investigation. This is joint work with George Andrews. |
| Affiliation: Michigan Tech |
| Video: | Video |
| Slides: | William Keith slides |
|
| Date: Mar 10 2022 | Title: Linked partition ideals and Schur's 1926 partition theorem |
| Speaker: Shane Chern | Abstract: Issai Schur's famous 1926 partition theorem states that the number of partitions of n into distinct parts congruent to ± 1 modulo 3 is the same as the number of partitions of n such that every two consecutive parts have difference at least 3 and that no two consecutive multiples of 3 occur as parts. In this talk, we consider some variants of Schur's theorem, especially their Andrews-Gordon type generating functions, from the perspective of span one linked partition ideals introduced by George Andrews. Our investigation has interesting connections with basic hypergeometric series, q-difference equations, computer algebra, and so on. |
| Affiliation: Dalhousie University |
| Video: | Video |
| Slides: | Shane Chern slides |
|
| Date: Mar 24 2022 | Title: Completing the A2 Andrews-Schilling-Warnaar identities |
| Speaker: Matthew Russell | Abstract: We study the Andrews-Schilling-Warnaar sum-sides for the principal characters of standard (i.e., integrable, highest weight) modules of A2(1). These characters have been studied recently by various subsets of Corteel, Dousse, Foda, Uncu, Warnaar and Welsh. We prove complete sets of identities for moduli 5 through 8 and 10, in Andrews-Schilling-Warnaar form. The cases of moduli 6 and 10 are new. Our methods depend on the Corteel–Welsh recursions governing the cylindric partitions and on certain relations satisfied by the Andrews–Schilling–Warnaar sum-sides. We speculate on the role of the latter in the proofs of higher modulus identities. Further, we provide a complete set of conjectures for modulus 9. We show that at any given modulus, a complete set of conjectures may be deduced using a subset of "seed" conjectures. These seed conjectures are obtained by appropriately truncating conjectures for the "infinite" level. Additionally, for moduli 3k, we use an identity of Weierstraß to deduce new sum-product identities starting from the results of Andrews-Schilling-Warnaar. Joint work with Shashank Kanade. |
| Affiliation: UIUC |
| Video: | Video |
| Slides: | Matthew Russell slides |
|
| Date: Apr 14 2022 | Title: Copartitions and Their Connections to Classical Partition-Theoretic Objects |
| Speaker: Dennis Eichhorn | Abstract: Copartitions are a generalization of partitions with connections to many classical topics in partition theory, including two-colored partitions, Rogers-Ramanujan partitions, partitions with parts separated by parity, and crank statistics. In this talk, we introduce copartitions and focus on these connections. This talk is joint work with Hannah Burson. |
| Affiliation: UC-Irvine |
| Video: | Video |
| Slides: | Dennis Eichhorn slides |
|
| Date: Apr 21 2022 | Title: Copartitions: Parity and Positivity |
| Speaker: Hannah Burson | Abstract: Copartitions are a generalization of partitions with connections to a wide range of partition-theoretic topics. Additionally, they provide combinatorial interpretations for the coefficients in the q-series expansions of a family of infinite products. In this talk, we discuss properties of those coefficients, with a special focus on what we know about parity and positivity. Though this talk can be thought of as a sequel to the talk last week, all needed definitions will be restated and no previous exposure to copartitions is necessary. This talk is joint work with Dennis Eichhorn. |
| Affiliation: Univ. of Minn. |
| Video: | Video |
| Slides: | Hannah Burson slides |
|
| Date: Apr 28 2022 | Title: A bijective proof and generalization of the non-negative crank-odd mex identity |
| Speaker: Isaac Konan | Abstract: Recent works of Andrews-Newman and Hopkins-Sellers unveil an interesting relation between two partition statistics, the crank and the mex. They state that, for a positive integer n, there are as many partitions of n with non-negative crank as partitions of n with odd mex. In this talk, we provide a generalization of this identity and prove it bijectively. Our method uses an alternative definition of the Durfee decomposition, whose combinatorial link to the crank was recently studied by Hopkins, Sellers, and Yee. |
| Affiliation: Université Claude Bernard Lyon 1 |
| Video: | Video |
| Slides: | Isaac Konan slides |
|
| Date: Sep 16 2021 | Title: Combinatorial Perspectives on Dyson's Crank and the Mex of Partitions |
| Speaker: Brian Hopkins | Abstract: Recently there have been several connections established between Dyson's storied crank and a newer partition statistic, now called the mex: the least positive integer that is not a part of the partition. We will revisit and extend these results with an emphasis on combinatorial proofs. One highlight is a generating function expression for the number of partitions with a bounded crank that does not include an alternating sum, which leads to a combinatorial interpretation involving types of Durfee rectangles. This includes joint work with James Sellers, Dennis Stanton, and Ae Ja Yee. |
| Affiliation: Saint Peters University |
| Video: | Video |
| Slides: | Brian Hopkins slides |
|
| Date: Sep 23 2021 | Title: Schmidt Type partitions and modular forms (joint work with Peter Paule) |
| Speaker: George Andrews | Abstract: In 1999, Frank Schmidt noted that the number of partitions of integers into distinct parts in which the first, third, fifth, etc. summands add to n is equal to p(n), the number of ordinary partitions of n. By invoking MacMahon's theory of Partition Analysis, we provide a context for this result which leads directly to many other theorems of this nature. |
| Affiliation: Penn State |
| Video: | Video |
| Slides: | George Andrews slides |
|
| Date: Sep 30 2021 | Title: Weight 3/2 moonshine for the Thompson group |
| Speaker: Maryan Khaqan | Abstract: In recent work, we characterize all infinite-dimensional graded modules for the Thompson group whose graded traces are certain weight 3/2 weakly holomorphic modular forms satisfying special properties. This is an instance of moonshine for the Thompson group. In this talk, I will demonstrate how we can use one such module to study the ranks of certain families of elliptic curves. In particular, while number theory's contribution to moonshine is plentiful, this talk demonstrates an example of how moonshine can be used to answer questions in number theory. SPECIAL TIME: Dr. Khaqan is connecting from Europe; this Seminar will be held 1 hour EARLIER than the usual time. |
| Affiliation: Stockholm University |
| Video: | Video |
| Slides: |
|
| Date: Oct 14 2021 | Title: On new modulo 8 cylindric partition identities |
| Speaker: Ali Uncu | Abstract: We will discuss new sum-product identities that emerged from the study of cylindric partitions. Cylindric partitions were defined by Gessel and Krattenthaler in 1997 in the context of non-intersecting lattice paths. These combinatorial objects later appeared naturally in many different contexts. Most recently, Corteel and Welsh re-derived the A2 Rogers-Ramanujan identities originally proven by Andrews, Schilling and Warnaar using cylindric partitions. In their paper, they presented a general recurrence relation for cylindric partitions which can be applied to any class of such partitions. In a joint effort, the speaker, Corteel and Dousse studied a different class of cylindric partitions. This study led to the discovery of many intriguing multisum-product identities. |
| Affiliations: Univ. of Bath & OEAW RICAM |
| Video: | Video |
| Slides: | Ali Uncu slides |
|
| Date: Oct 21 2021 | Title: Product-sum identities from certain restricted plane partitions |
| Speaker: Walter Bridges | Abstract: A cylindric partition is a sort of restricted plane partition that can be thought of as wrapping around the surface of a cylinder. A profile describes their shape, and Borodin proved that for every profile, the generating function is a (modular) infinite product. Recently, Corteel and Welsh proved systems of recurrences for cylindric partitions of all profiles and found sum generating functions that solve these in several cases, thus establishing new connections between product-sum identities and an important combinatorial object.
We discuss an extension of Corteel-Welsh's work to symmetric cylindric and double skew shifted plane partitions, which, thanks to recent work of Han and Xiong, also come with infinite product generating functions. This is joint work with Ali Uncu. |
| Affiliation: Universität zu Köln |
| Video: | Video |
| Slides: | Walter Bridges slides |
|
| Date: Oct 28 2021 | Title: Generating Functions for Certain Weighted Cranks(joint work with Ae Ja Yee) |
| Speaker: Shreejit Bandyopadhyay | Abstract: Recently, George Beck posed many interesting partition problems considering the number of ones in partitions. In this talk, we first consider the crank generating function weighted by the number of ones and obtain analytical formulas for this weighted crank function under conditions of the crank being less than or equal to some specific integer. We connect these functions to the generating functions of partitions with certain sizes of Durfee rectangles. We then consider a generalization of the crank for k-colored partitions, and investigate the generating function for this generalized crank weighted by the number of parts in the first subpartition of a k-colored partition. We show that the cumulative generating functions in this case are the same as the generating functions for certain unimodal sequences. |
| Affiliation: Penn State |
| Video: | Video |
| Slides: | Shreejit Bandopadhyay slides |
|
| Date: Nov 4 2021 | Title: Proofs of Berkovich and Uncu's Conjectures on Integer Partitions using Frobenius Numbers |
| Speaker: Damanvir Singh Binner | Abstract: We use techniques from elementary number theory (such as Frobenius numbers) to combinatorially prove four recent conjectures of Berkovich and Uncu (Ann. Comb. 23 (2019) 263-284) regarding inequalities between the sizes of two closely related sets consisting of integer partitions whose parts lie in the interval {s, ..., L + s}. Further restrictions are placed on the sets by specifying impermissible parts as well as a minimum part. |
| Affiliation: IISER Mohali |
| Video: | Video |
| Slides: | Damanvir Singh Binner slides |
|
| Date: Nov 11 2021 | Title: Plane Partition Congruences and Localization |
| Speaker: Nicolas Smoot | Abstract: George Andrews and Peter Paule recently conjectured an infinite family of congruences mod powers of 3 for the 2-elongated plane partition function d2(n). This congruence family appears difficult to prove by classical methods. We prove a refined form of this conjecture by expressing the associated generating functions as elements of a ring of modular functions isomorphic to a localization of $\mathbb{Z}[X]$. This is a superb example of the utility of localization techniques to proving partition congruences. |
| Affiliation: RISC-Linz |
| Video: | Video |
| Slides: | Nicolas Smoot slides |
|
| Date: Nov 18 2021 | Title: Compositions from Ferrers Diagrams |
| Speaker: George Beck | Abstract: Think of the dots of the Ferrers diagram of an integer partition of n as a subset F of the lattice points in the plane. Let L be the set of lines l of rational slope s passing through the convex hull of F and a lattice point. Count the points of F that lie on each line of L (starting with the line with greatest y intercept) to form a composition of n. We present conjectures about the enumeration of various statistics for sets of such compositions. |
| Affiliation: Wolfram Research |
| Video: | Video |
| Slides: | Pdf of talk notebook, Executable talk notebook, CORE 6 notebook with auxiliary functions |
|
| Date: Dec 2 2021 | Title: Semi-Modular Forms |
| Speaker: Robert Schneider | Abstract: We introduce our developing theory of a new class of functions that complement modular forms, that are "half-modular" in a specific sense. Using variations on classical Eisenstein series involving integer partitions and also Lucas sequences, we construct first examples of semi-modular forms, and conjecture what other examples might look like. (Joint work with A. P. Akande and M. Just) |
| Affiliation: Univ. of Georgia |
| Video: | Video |
| Slides: | Robert Schneider slides |
|
| Date: Dec 9 2021 | Title: Congruences for k-elongated partition diamonds |
| Speaker: James Sellers | Abstract: In 2007, George Andrews and Peter Paule published the eleventh paper in their series on MacMahon's partition analysis, with a particular focus on broken k-diamond partitions. On the way to broken k-diamond partitions, Andrews and Paule introduced the idea of k-elongated partition diamonds. Recently, Andrews and Paule revisited the topic of k-elongated partition diamonds in a paper that is to appear in the Journal of Number Theory. Using partition analysis and the Omega operator, they proved that the generating function for the partition numbers dk(n) produced by summing the links of k-elongated plane partition diamonds of length n is given by (q2;q2)∞k/(q;q)∞3k+1 for each k ≥ 1. A significant portion of their recent paper involves proving several congruence properties satisfied by d1, d2 and d3, using modular forms as their primary proof tool. Since then, Nicolas Smoot has extended the work of Andrews and Paule, refining one of their conjectures and proving an infinite family of congruences modulo arbitrarily large powers of 3 for the function d2.
In this work, our goal is to extend some of the results proven by Andrews and Paule in their recent paper by proving infinitely many congruence properties satisfied by the functions dk for an infinite set of values of k. The proof techniques employed are all elementary, relying on generating function manipulations and classical q-series results.
This is joint work with Robson da Silva of Universidade Federal de Sao Paulo (Brazil). |
| Affiliation: UMN-Duluth |
| Video: | Video |
| Slides: | James Sellers slides |
|
| Date: Feb 18 2021 | Title: Identities of Hecke type and Rogers-Ramanujan type |
| Speaker: Shane Chern | Abstract: In this talk, I will present several basic hypergeometric transformations from which dozens of identities of Hecke type and Rogers-Ramanujan type would be deduced. The results come from my joint papers with Chun Wang. |
| Affiliation: Penn State |
| Video: | Video |
| Slides: | Shane Chern slides |
|
| Date: Feb 25 2021 | Title: 5-adic Convergence Over Modular Curves of Genus 1: The Andrews--Sellers Congruences and Beyond |
| Speaker: Nicolas Smoot | Abstract: A major topic of interest in the theory of partitions is the study of infinite families of congruences---regular patterns of divisibility of a given partition function by arbitrarily large powers of a given prime. In the century since Ramanujan's groundbreaking work on this subject, our understanding has grown substantially. A notable feature of this subject is the considerable range in the difficulty of proving a given congruence family. Possible complications include the genus of the underlying modular curve, issues in the representation of the associated family of modular functions, and more subtle matters involving piecewise p-adic convergence. In this talk we will discuss these complications, together with some recent techniques in proving congruence families, as well as the prospect of an algorithmic framework for studying them. |
| Affiliation: RISC |
| Video: | Video |
| Slides: | Nicolas Smoot slides |
|
| Date: Mar 4 2021 | Title: Under construction: a multiplicative theory of integer partitions |
| Speaker: Robert Schneider | Abstract: Pdf link |
| Affiliation: Univ. of Georgia |
| Video: | Video |
| Slides: | Robert Schneider slides, extended notes |
|
| Date: Mar 18 2021 | Title: The Unimodularity of Gaussian polynomials $N+m\brack m$ for a few small values of $m$ |
| Speaker: Brandt Kronholm | Abstract: In this talk I will give a proof of the unimodularity of Gaussian polynomials $N+4\brack 4$, $N+3\brack 3$, and $N+2\brack 2$. The proof will come from an examination of a collection of generating functions for these Gaussian polynomials. (TeX pdf abstract) |
| Affiliation: Univ. of Texas-RGV |
| Video: | Video |
| Slides: | Brandt Kronholm slides |
|
| Date: Mar 25 2021 | Title: Distribution of partition statistics in arithmetic progressions |
| Speaker: Ken Ono | Abstract: Recent works at the interface of algebraic geometry, number theory, representation theory, and topology have provided decompositions of the set of size n integer partitions. The examples we consider arise from extensions of the Nekrasov-Okounkov and Han hook product formulas, and the study of Betti numbers of various n point Hilbert schemes. In analogy with Dirichlet's Theorem on primes in arithmetic progressions, we sort the size n partitions by congruence conditions on the relevant partition invariants. For the Hilbert schemes, we prove that homology is equidistributed for large n. For t-hooks in Ferrers-Young diagrams, we prove distributions which are often non-uniform. The cases where t ∈ {2, 3} stand out, as there are congruence classes where such counts are identically zero!
This is joint work with Kathrin Bringmann, Will Craig, and Joshua Males. |
| Affiliation: Univ. of Virginia |
| Video: | Video |
| Slides: | Ken Ono slides |
|
| Date: Apr 1 2021 | Title: Sequentially Congruent Partitions and Partitions into Squares |
| Speaker: James Sellers | Abstract: In recent work, Max Schneider and Robert Schneider studied a curious class of integer partitions called "sequentially congruent" partitions wherein the mth part is congruent to the (m+1)st part modulo m, and the smallest part is congruent to zero modulo the number of parts in the partition. After sharing a number of results that Schneider and Schneider proved regarding these sequentially congruent partitions, we will then prove that the number of sequentially congruent partitions of weight n is equal to the number of partitions of weight n where all parts are squares. We then show how our proof naturally generalizes to other classes of partitions where the parts are all kth powers for some fixed k. This is joint work with Robert Schneider and Ian Wagner. |
| Affiliation: Univ. of Minn.-Duluth |
| Video: | Video |
| Slides: | James Sellers slides |
|
| Date: Apr 8 2021 | Title: Partition Eisenstein series and semi-modular forms |
| Speaker: Matt Just | Abstract: We identify a class of "semi-modular" forms invariant on special subgroups of GL2(ℤ), which includes classical modular forms together with complementary classes of functions that are also nice in a specific sense. We define an Eisenstein-like series summed over integer partitions, and use it to construct families of semi-modular forms. We ask whether other examples exist, and what properties they all share. |
| Affiliation: UGA |
| Video: | Video |
| Slides: | Matthew Just slides |
|
| Date: Apr 15 2021 | Title: A poset of generating functions of partitions of n |
| Speaker: Tim Wagner | Abstract: In this talk, we present our work on a novel poset: Pn ={Gλ | λ ⊢ n}, the poset of generating functions of partitions of n. The motivation behind this poset is an intriguing and beautiful conjecture by François Bergeron. Our strongest result on this poset is that two "balancing" operations on the principal hooks of a partition λ produce generating functions at least as large as Gλ (in the ordering of Pn). This imposes a strong necessary condition on the maxima of Pn. We conjecture an asymptotic value of |Pn|, and show that determining |Pn| exactly appears to be nontrivial. This we demonstrate by providing an infinite family of non-conjugate pairs of partitions that have the same generating function. Finally, we discuss asymptotic results on the number of maxima in this poset. |
| Affiliation: MTU |
| Video: | Video |
| Slides: | Tim Wagner slides |
|
| Date: Apr 29 2021 | Title: A bijection for partitions into parts simultaneously s-regular and t-distinct |
| Speaker: William J. Keith | Abstract: We consider partitions simultaneously satisfying two different restrictions from the classic theory. We construct a bijection which realizes the main symmetry of the class and ask about its characteristics, and whether the bijection can be improved. We are particularly interested in the place of Glaisher's map in the problem. This is work in progress and ideas are welcome. |
| Affiliation: Michigan Tech |
| Video: | Video |
| Slides: | William Keith slides |
|
| Date: May 6 2021 | Title: Gupta, Ramanujan, Dyson, and Ehrhart: Formulas for Partition Functions, Congruences, Cranks, and Polyhedral Geometry |
| Speaker: Joselyne Rodriguez | Abstract: We will revisit Gupta's 1975 result regarding properties of formulas for restricted partitions with the goal of generalizing the result. We will then use this result to prove an infinite family of Ramanujan-style partition congruences. We find and prove combinatorial witnesses, also known as cranks, for the congruences using polyhedral geometry. |
| Affiliation: Univ. of Texas-RGV |
| Video: | Video |
| Slides: | Joselyne Rodriguez slides |
|



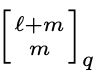 , as polynomials in q. They showed it to be true for all ℓ, m ≥ 8 and a few other cases. We propose a different approach to this problem based on computer algebra, where we establish a closed form for the coefficients of these polynomials and then use cylindrical algebraic decomposition to identify exactly the range of coefficients where strict unimodality holds. This strategy allows us to tackle generalizations of the problem, e.g., to show unimodality with larger gaps or unimodality of related sequences. In particular, we present proofs of two additional cases of a conjecture by Stanley and Zanello.
, as polynomials in q. They showed it to be true for all ℓ, m ≥ 8 and a few other cases. We propose a different approach to this problem based on computer algebra, where we establish a closed form for the coefficients of these polynomials and then use cylindrical algebraic decomposition to identify exactly the range of coefficients where strict unimodality holds. This strategy allows us to tackle generalizations of the problem, e.g., to show unimodality with larger gaps or unimodality of related sequences. In particular, we present proofs of two additional cases of a conjecture by Stanley and Zanello.